五、广义积分

       １. 广义积分的概念

       ［无穷限广义积分］  设函数f(x)在[a,b]上可积，u>a,<b,u>,当下列各式右边的极限存在时，

这时称无穷限广义积分收敛，否则称为发散.

       [无界函数的广义积分]  设函数f(x)在给定区间[a,b]上只有一个瑕点x=c,即函数f(x)在x=c点的邻域内无界，而在[a,c-ε]及[c+ε',b]上可积，ε，ε'为任意小的正数，当ε和ε'独立地趋于零，极限

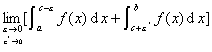                                           (1)

存在时，则用上式定义无界函数f(x)从a到b的瑕积分，记作

       [柯西主值]  有时极限（1）不存在，但如果设ε'=ε→0，这个极限（1）存在，就称它为瑕积分的主值，记作

这时称无界函数广义积分在主值意义下收敛，否则称为发散.

       [绝对收敛与条件收敛]  如果f(x)的广义积分与|f(x)|的广义积分同时收敛，那末称f(x)的广义积分是绝对收敛, f(x)称为绝对可积；如果仅前者收敛，后者不收敛，那末称f(x)的广义积分是条件收敛.