§6 二 次 曲 面
一、 球面
[球面的方程、球心与半径]
|
方 程 与 图 形 |
球心与半径 |
||
|
或
(球面坐标方程.式中j为经度,q为余纬度) |
|
球心 G(0,0,0) 半径 R |
|
|
或 (球面坐标方程式中j,q 同上) |
|
球心 G(a,b,c) 半径 R |
|
|
方 程 与 图 形 |
球心与半径 |
||
|
|
球心 半径
|
||
[球面的切面与法线] 设一平面P通过球面上一点M且垂直于半径GM,则称P为球面在M的切面.直线MG称为球面在点M的法线.
设球面方程为
![]()
则球面在点M(![]() )的切面方程为
)的切面方程为
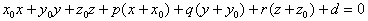
球面在点M(![]() )的法线方程为
)的法线方程为
![]()
[两个球面的交角] 设两个球面
![]() =0
=0
![]() =0
=0
两个球面的交角是指它们在交点的两个切面的夹角,记作q,则
![]()
因公式中不包含交点的坐标,所以在两个球面的交线上的各点的交角必相等.
两个球面的正交条件为
![]()
[球面束·两个球面的根面] 设
![]()
式中![]() 和
和![]() 如(1)式定义,
如(1)式定义,![]() 为参数,则有
为参数,则有
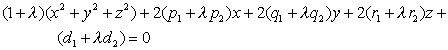
对![]() 的一个确定值,
的一个确定值,![]() 表示一个球面,当
表示一个球面,当![]() 取一切值
取一切值![]() 时,
时,![]() 所表示的球面的全体称为球面束.
所表示的球面的全体称为球面束.![]() 时为一平面,称为两个球面
时为一平面,称为两个球面![]() 的根面,其方程为
的根面,其方程为
![]()
根面与![]() 和
和![]() 的连心线垂直,束中任一球面
的连心线垂直,束中任一球面![]() 的中心在连心线上,且分连心线的比为
的中心在连心线上,且分连心线的比为![]() .
.
[球面汇·三个球面的根轴] 设![]() 和
和![]() 如(1)式定义,又设
如(1)式定义,又设
![]()
设
![]()
式中![]() 为二独立参数,则有
为二独立参数,则有
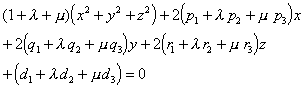
对![]()
![]() 的一对确定值,
的一对确定值,![]() 表示一个球面,当
表示一个球面,当![]() 取一切值
取一切值![]() 时,
时,![]() 所表示的球面的全体称为球面汇.
所表示的球面的全体称为球面汇.
三个球面中每对球面的根面分别为
![]() 和
和![]()
这三个平面交于一条直线,称为![]() 的根轴.
的根轴.






