二、快速傅立叶变换算法
快速傅立叶变换算法(简称FFT算法)是计算有限离散傅立叶变换的快速方法.
[复序列的FFT算法] 计算复序列{zk} ![]() 的有限离散傅立叶变换
的有限离散傅立叶变换![]() ,就是计算形如
,就是计算形如
,
的有限项和.对于反演公式,计算的方法类似.
设N=2m,
![]() ,
那末
,
那末
![]()
又设
![]()
![]()
分别是k和j的二进制表示,![]() 取值为0或1,
取值为0或1,![]() .那末
.那末
![]()
因为 ![]() =
=
![]()
=![]()
=![]()
所以
![]()
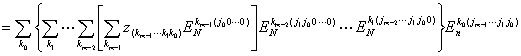
从而得出递推公式:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
最后有
![]()
[实序列的FFT算法] 设有2N (N=2m)个元素构成的实序列![]()
![]() 要计算
要计算![]() 的有限离散傅立叶余弦变换和正弦变换
的有限离散傅立叶余弦变换和正弦变换
![]()
![]()
![]()
![]()
可先用FFT算法关于复序列
zk=xk+iyk ![]()
计算
![]()
而 cj , sj 用下列公式去求

![]()
至于cj , sj 当![]() 的数值是
的数值是