§3   曲线拟合的圆弧法与平均法

一、曲线拟合的圆弧法

圆弧拟合是一种描绘通过观测点(型值点)的拟合曲线的几何方法。它用分段圆弧代替曲线，并且使相邻两个圆弧有公共切线。这个方法归结为下面三种情形:

   已知圆O和圆外两点，,求圆P，使它通过点，并且与圆O相切(外切或内切)(图17.2)。

 设圆O的半径为r，O点的坐标为(0,0)。记

                             

       

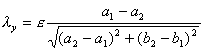
，符号视内切或外切而定。又记

           

式中

           

           

           

那末

(i) 圆P的圆心坐标为

                

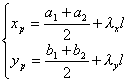
(ii) 圆P的半径R为

        

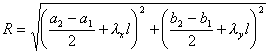
(iii) 切点的坐标为

         

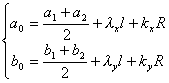
其中 

            

            

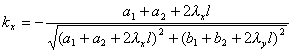
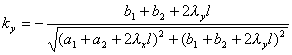
  已知圆Q和圆外一点，求圆P，使它通过定点，并且和圆Q切于定点(图17.3)。

   设圆Q的圆心坐标为(s,t)，那末

(i) 圆P的圆心坐标为

  

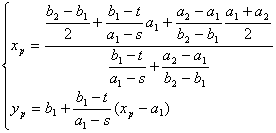
(ii) 圆P的半径R为

          

   已知圆Q和圆，求圆P，使它和圆相切，且与圆Q切于定点 (图17.4)。

 设圆Q的圆心坐标为(s,t)，半径为r；圆的圆心坐标为，半径为。又记

      

         

         

         

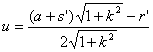
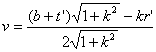
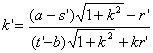
那末

(i) 圆P的圆心坐标为

            

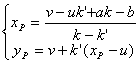
(ii) 圆的半径R为

            

(iii) 切点A’的坐标(x’,y’)为

            

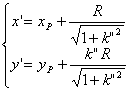
式中