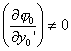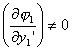三.可动边界的泛函的极值
![]()
![]() 型泛函的可动边界问题
型泛函的可动边界问题![]()
1°
若![]() 两端点分别在曲线
两端点分别在曲线![]() 和
和![]() 上变动,则使泛函达到极值的函数
上变动,则使泛函达到极值的函数![]() ,除必须满足欧拉方程
,除必须满足欧拉方程
![]()
外,其端点还必须满足所谓横截条件
![]()
![]()
2° 若![]() 两点所在曲线以隐函数形式给出:
两点所在曲线以隐函数形式给出:
![]()
![]()
其中![]() 有连续的偏导数,且
有连续的偏导数,且
 ,
,
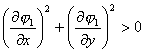
则横截条件为
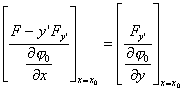
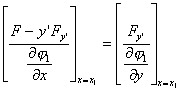
![]() 型泛函的可动边界问题
型泛函的可动边界问题![]()
1°
若![]() 两端点分别在曲线
两端点分别在曲线
 和
和 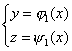
上变动,则使泛函达到极值的函数![]() ,除必须满足欧拉方程
,除必须满足欧拉方程
![]()
![]()
外,其端点还必须满足横截条件
![]()
![]()
2° 若![]() 分别在曲面
分别在曲面
![]() 和
和
![]()
上变动,则横截条件为
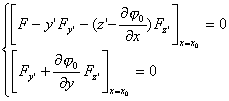
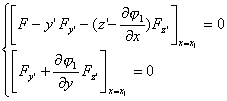
![]() 型泛函的可动边界问题
型泛函的可动边界问题![]()
1° 若![]() 之间满足关系
之间满足关系
![]()
![]() 之间满足关系
之间满足关系
![]()
则使泛函达到极值的函数![]() ,除必须满足欧拉方程
,除必须满足欧拉方程
![]()
外,其端点还必须满足横截条件
![]()
![]()
2° 如果![]() 满足关系式
满足关系式![]() ,
,![]() 满足关系式
满足关系式![]() ,则横截条件为
,则横截条件为