§4 数论函数
对任一正整数n有确定值的函数f(n)称为数论函数.
[积性函数与完全积性函数] 若(m,n)=1,有f(mn)=f(m)f(n),则称数论函数f(n)为积性函数.若对任意正整数m,n都有f(mn)=f(m)f(n),则称f(n)为完全积性函数.
积性函数具有下列性质:
1° 若f(n)为非零积性函数,则f(1)=1.
2° 若g(n),h(n)都为积性函数,则g(n)h(n)仍为积性函数.且
![]()
也为积性函数,这里å是对n的所有不同因数d求和.
3° 若g(n)为非零积性函数,且![]() ,则
,则
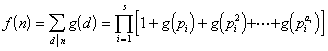
也为积性函数.
4° 若f(n)为积性函数,则
f([m,n])f((m,n))=f(m)f(n)
式中(m,n)为m,n的最大公因数,[m,n]为m,n的最小公倍数.
[麦比乌斯函数] 函数

称为麦比乌斯函数.
麦比乌斯函数具有下列性质:
1° 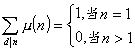
2° μ(n)为积性函数,但非完全积性函数.
3° 设![]() ,若f(n)为积性函数,则
,若f(n)为积性函数,则
![]()
![]()
也为积性函数.例如
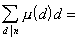
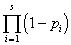
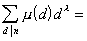
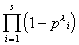
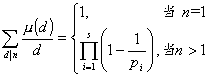
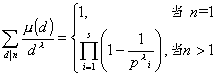
[欧拉函数] 设n为自然数,![]() (n)为不超过n且与n互素的正整数的个数,称为欧拉函数.
(n)为不超过n且与n互素的正整数的个数,称为欧拉函数.
欧拉函数具有下列性质:
1° ![]() (n)为积性函数,但非完全积性函数.
(n)为积性函数,但非完全积性函数.
2° 若![]() ,则
,则
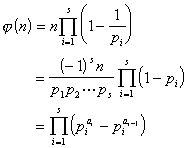
特别,当p为素数时,
![]()
3° ![]()
4° 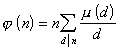
[除数函数] 自然数n的全部因数的个数称为除数函数,记作d(n).除数函数具有下列性质:
1° d(n) 为积性函数,但非完全积性函数,对任意自然数m,n,常有
![]()
2° 若![]() ,则
,则
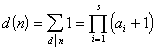
[冯·曼哥特函数] 函数
L (n)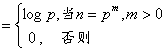
称为冯·曼哥特函数.L (n)非积性函数.
[麦比乌斯反转公式与麦比乌斯变换]
1° 反转公式一 设![]() ,又设h(k)为一非零完全积性函数.若对所有适合于
,又设h(k)为一非零完全积性函数.若对所有适合于![]() 的h常有
的h常有
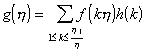
则对上述h也常有
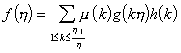
反之也真.
2° 反转公式二 设![]() ,又设H(k)为一非零完全积性函数.若对所有适合于
,又设H(k)为一非零完全积性函数.若对所有适合于![]() 的x 常有
的x 常有
![]()
则对上述x 也常有
![]()
反之也真.
3° 反转公式三 设![]() 为一正整数, 又设h(k)为一非零完全积性函数.若对所有
为一正整数, 又设h(k)为一非零完全积性函数.若对所有![]() 常有
常有
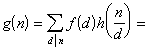
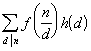
则对上述n也常有
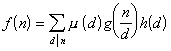
反之也真.
4° 麦比乌斯变换 设n为正整数,若
![]()
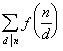
则
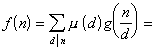
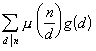
g(n)称为f(n)的麦比乌斯变换,f(n)称为g(n)的麦比乌斯逆变换.
5° 乘积麦比乌斯变换 设n为正整数,若
![]()
则
![]()
g(n)称为f(n)的乘积麦比乌斯变换,f(n)称为g(n)的乘积麦比乌斯逆变换.
[麦比乌斯变换表]
![]()
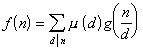
|
g(n) |
f(n) |
|
|
|
|
|
|
|
1 |
|
|
d(n) |
1 |
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
L (n) |
- |
|
logn |
L (n) |