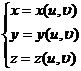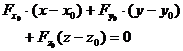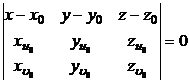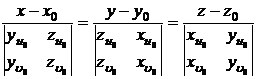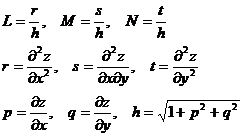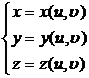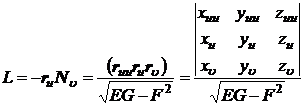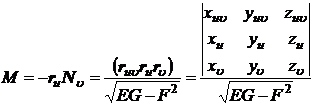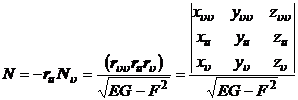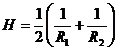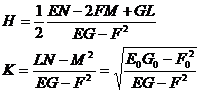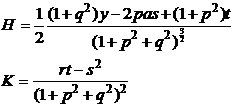§ 12 一般曲面

一、曲面的方程与曲线的坐标

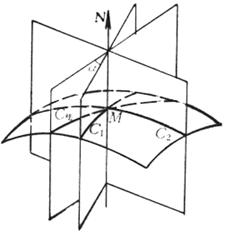
图 7.23

曲面方程的形式有

隐 式 F(x,y,z)=0

显 式 z=f(x,y)

参数式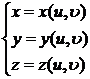

矢量式 r=r(u,)

或 r=x(u,)i+y(u,)j+z(u,)k

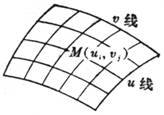
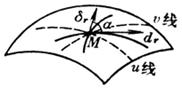
对于参数式或矢量式表示的曲面，如果取为一系列数值L，而让u连续变动，则r(u,)(i=1,2,L)表示一族曲线，称为u线（图7.23）；同样，如果取u为一系列数值u₁,u₂,L，而让连续变动，则r(u_i,)(i=1,2,L)表示另一族连续曲线，称为线.u线与线在曲面上构成曲线网，称为坐标线或坐标网.于是u=u_i, =这个数对就可以确定曲面上一点M，这数对(u_i,)称为点M的曲线坐标（或高斯坐标）.

二、 切面、法线与曲面的方向

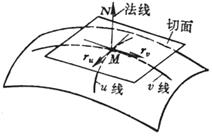
[法线单位矢量] 通过曲面上一的M所有曲面曲线（即该曲面上的曲线），在点M的切线落在同一平面上（奇点除外），称这平面为曲面在点M的切面通过点M与切面垂直的直线称为曲面在点M的法线.

切面通过的矢量

r_u=和

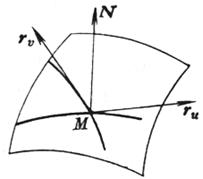
称为坐标矢量，它们分别是u线和线在点M的切矢量（图7.24）

图 7.24

曲面上点的法线单位矢量为

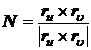
这里为了区别曲线的法线单位矢量和曲面的法线单位矢量，前者以n表示，后者以N表示.

[曲面的方向] 曲面的方向规定如下：朝N的正向那一面是曲面的正面（图7.24中看到的一面）；另一面为反面.

[曲面的切线方程与法线方程]

曲面方程	切面方程	法线方程
z=f(x,y) r=r(u,)	或(r-r0)N0=0	或 式中为参数

表中分别表示在点M(x₀,y₀,z₀)的值，r₀是点M的矢径，分别表示在点M的值，N₀为点M的法线单位矢量.

[曲面的奇点] 若曲面F(x,y,z)=0上一点M(x₀,y₀,z₀)的三个偏导数同时等于零，即

则称点M为该曲面的奇点.

三、 第一基本二次型与曲面的度量

[第一基本二次型与第一基本量]

曲面方程	第一基本二次型与第一基本量
z=f(x,y) 或 r=r(u,)	ds^2=Edx^22fdxdy+Gdy^2 式中 E=1+ F= G=1+ ds为点M(x,y,z)处的弧的微分，ds^2称为第一基本二次型，E,F,G称为第一基本量 ds^2==Edu^2+2Fdud+Gd^2 式中 E= F= G= 第一基本量E,F,G都在点M处取值. 曲面上每点（奇点除外）的第一基本二次型是正定的，即 E>0,G>0,EG-F^2>0

[曲面上的弧长、面积、夹角等计算公式]

各量与图形	计算公式
曲面曲线的弧长L 曲面面积S （由曲线围成） 曲线夹角（两条曲线交于点M）
式中 E，F，G为曲面的第一基本量（在点M取值）。坐标线u=常数和v=常数的交角决定于 因此坐标线正交的充分必要条件是：

[曲面的变形] 保持曲面曲线长度不变的变换称为曲面的变形。具有相同的第一基本二次型的两个曲面S，称为贴合的或等距的。从S到和从到S的这种变换都称为等距变换。关于曲面的几何量经过等距变换不变者都称为等距不变量。

等距变换的一种具体表现是把一个曲面连续弯曲而保持曲面曲线的长度不变，使这个曲面最后与另一个曲面相贴合；因此，等距变换又称为变形。

从定义可以推出，两个曲面互为变形的充分必要条件是：经过适当地选择参数后，它们具有相同的第一基本二次型。

四、第二基本二次型曲面曲线的曲率

[第二基本二次型与第二基本量]

曲 面 方 程	第二基本二次型与第二基本量
	式中
曲 面 方 程	第二基本二次型与第二基本量
或	称为第二基本二次型，L，M，N称为第二基本量 式中偏导数等在点取值，E，F，G为第一基本量，N为曲面在点M的法线单位矢量。 表示曲面上两个无限邻近点中，一点到另外一点的切面的距离的主要部分的两倍，它表明曲面与切面的离差的特征，也反映曲面在空间中的弯曲程度

图 7.25

[主法截线（主方向、主曲率半径与脐点）] 通过曲面上一点M的法线的平面与曲面的交线（）都称为点M的法截线。所以通过曲面上一点的法截线有无穷多条，给定点M的一个切线方向就有一条确定的法截线。在点M的法截线中曲率最大和最小的两条分别记为，它们称为主法截线，在点M所对应的切线方向称为主方向，这两个方向互相垂直。的曲率半径（）称为主曲率半径，它们等于下列方程的两个根：

对于曲面，方程为

式中p，q，r，s，t，h见上页表。

对于曲面，方程为

式中E，F，G为曲面的第一基本量，L，M，N为曲面的第二基本量。

主曲率半径相等的点称为曲面的脐点，在脐点上

[曲率线与罗德里克公式] 主方向是二次方程

的两个根。满足这个微分方程的曲面曲线称为曲率线。曲率线上每点的切线方向都是主方向，曲率线构成曲面上一个正交曲线网，曲率线还有如下的一个特征：

一条曲面曲线C是曲率线的充分必要条件是：沿C的曲面法线组成一个可展曲面，即当C上的点M变动时，曲面在M点的法线有包络线。

这个特征也可表示为

这个公式称为罗得里克公式。

五、 曲面曲线的曲率半径

[法截线的曲率半径与欧拉公式] 设

右边为正时，表示法截线的法线单位矢量n与曲面的法线单位矢量N一致，则法截线的曲率半径为；右边为负时，表示n与N相反，则法截线的曲率半径为。

若通过法截线的截平面与通过主法截线的截平面之间的夹角为，则

式中为主曲率半径，称为法曲率，这个等式称为欧拉公式。

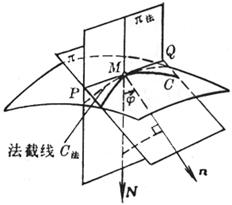
图 7.26

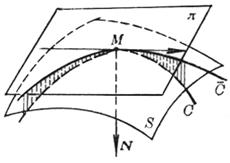
[任意平截线的曲率半径] 用通过点M的任意平面截曲面得截线C（图），它在点M的切线为PQ，曲线C的法线单位矢量为n，通过直线PQ和曲面的法线单位矢量N作意平面，截曲面得法截线。若矢量N与n夹角为，而的曲率半径为，则截线C的曲率半径为

（1）

[曲面上任意曲线的曲率半径与梅尼埃定理]

设曲面上任意曲线B上一点M的密切面与曲面交线为C，则曲面B的曲率半径等于截线C的曲率半径，于是从式（1）得到梅尼埃定理：曲面上任意曲线B的曲率半径等于在曲面法线上所截取的对应法截线的曲率半径在曲线B的主法线上的正射影。

六、 第三基本二次型与曲面的曲率

[第三基本二次型与第三基本量]

称为第三基本二次型，式中N为曲面的法线单位矢量，

称为第三基本量。

[曲面的平均曲率与总曲率（或高斯曲率）]

曲面方程	曲率定义	公式
	主曲率的平均数称为曲率，记作H， 主曲率的乘积称为总曲率（或高斯曲率），记作K，
		式中p，q，r，s，t见前表

注：1、，H和K都是曲面上点的函数，与所取的曲线坐标u，无关。

2、的点称为椭圆点，这种点邻近的曲面在该点切面的同侧；的点称为双曲点，这种点邻近的曲面象马鞍形；的点称为抛物点，这种点邻近的曲面象半马鞍形。

3、三个基本二次型有如下的线性关系：

或

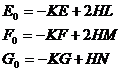
七、 渐近曲线、共轭曲线与极小曲面

[渐近曲线] 在曲面上一点的法曲率等于零的方向称为渐近方向。假定一条曲面曲线C上所有点的切线方向都是渐近方向，则称C为曲面的一条渐近曲线。是渐近方向的条件是第二基本二次型等于零：

或

这就是渐近曲线的微分方程。这种曲线有一个简单的几何特征：

渐近曲线的密切面与曲面一致。

由此可见，渐近曲线在其上一点与曲面构成二阶接触。

此外还有爱涅勃定理：

渐近曲线的挠率，K为曲面的总曲率（时，无渐近曲线）。

[共轭曲线] 在曲面上一点的两个方向与满足

则称它们互为共轭方向。

渐近方向是自己共轭的。

曲面上一条曲线C的切面族的特征线的方向为C的切线的共轭方向。

满足上面的微分方程的两族曲线构成的网称为共轭网。

[极小曲面] 平均曲率的曲面称为极小曲面，它也可定义为张在已知边界上面积最小的曲面。一个曲面为极小曲面的充分必要条件是：渐近曲线构成正交网。

注意：坐标线（u=常数和=常数）是共轭的充分必要条件是：；坐标线是曲率线的充分必要条件是：；坐标线是渐近曲线的充分必要条件是：。

八、 曲面的基本公式与基本方程

[高斯公式与外因格尔登公式] 设曲面的参数方程为，在曲面上每点M取三个不共面的矢量，由这三个矢量组成的三面形称为曲面的活动标架或伴随三面形；要注意，在这里和不互相垂直，但它们都在切面上而垂直于法线单位矢量N.

图 7.27

可以把关于u，的偏导数表示为下列形式的线性组合：

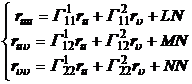（1）

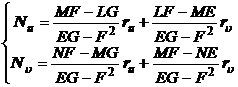（2）

式中E，F，G和L，M，N分别为曲面的第一和第二基本量；六个系数称为第一基本二次型的第二类克里斯托弗尔记号，它们的表达式是

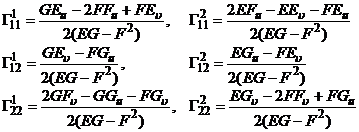
方程组（1）称为曲面的偏微分方程，又称为高斯公式；方程组（2）称为外因格尔登公式；（1），（2）合称为曲面的基本公式，这些公式的特点是，把矢量的导数用矢量本身的线性组合来表达，其系数仅与曲面的第一、第二基本量有关.

[高斯方程与柯达奇方程] 方程组（1）的可积条件为

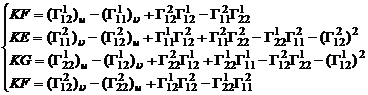（3）

和

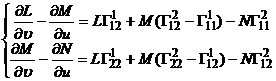（4）

方程组（2）的可积条件是（4）.方程组（4）成为柯达奇方程.

从（3）可以得到下列定理：

1、高斯定理 曲面的总曲率K可以用第一基本量和它们的一阶，二阶偏导数来表示；因而总曲率是曲面的一个等距不变量.

2、在等距对应下，曲面的对应点必有相同的总曲率.

这个重要结果表明，总曲率不同的两个曲面具有很大的差别性，即使允许曲面经过任意的弯曲，也不能使这两个曲面互相贴合.

总曲率K以E，F，G的表达式称为高斯方程，与柯达奇方程合并起来称为曲面的基本方程.

图 7.28

[波恩涅定理] 给定任意两个二次型

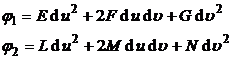
其中是正定的，假定和的系数满足高斯方程和柯达奇方程，则除了空间位置的差别外，唯一地存在一个曲面，以和分别作为它的第一和第二基本二次型.

九、 曲面曲线的测地曲率、测地线与测地坐标

[测地曲率与贝尔特拉米公式] 设M为曲面S上一点，C为S上通过点M的一条曲线，为S在M的切面，为C在上的正射影，则在M的曲率称为C在M的测地曲率，记作.

设曲面S的参数方程为，曲面曲线C的方程为，则C的测地曲率

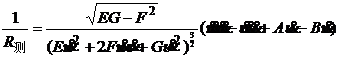（1）

式中

如果曲线C以弧长s为参数，则

（2）

式中

公式（1）和（2）称为测地曲率的贝尔特拉米公式.

测地曲率是等距不变量.

[测地线] 如果一条曲面曲线C上每点的测地曲率都等于零，则称C为曲面上的一条测地线.

测地线的微分方程是

也可写为

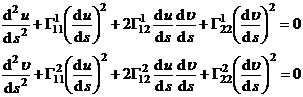
或

对于曲面上的测地线的微分方程为

式中p，q，r，s，t 见前表.

测地线具有性质：

1、测地线在每点M的曲率小于与它在M相切的任何曲线在M的曲率.

2、如果把曲面曲线C的可展曲面变成平面时，那末只有测地线所对应的曲线是直线.

3、一条曲面曲线C是测地线的充分必要条件是：在C上每点的主法线与该点的曲面法线重合，即C的密切面包含曲面法线.

4、如果两个曲面沿一共同曲线C相切，假设C是其中一个曲面的测地线，则C也是另一个曲面的测地线.

5、通过曲面上每点沿每一方向有一条且有一条测地线.

6、在充分小的邻域里，测地线是短程线，即连接曲面上两个邻近点的一切曲面曲线中，测地线的长度最短.

[测地坐标] 若取坐标线u=常数为测地线=常数的正交轨线，则称为测地坐标，这族正交轨线称为测地平行线，这时

以测地坐标表示的总曲率为

若测地线=常数交于一点O，表示测地线和测地线的交角，则称为测地极坐标，这时的测地平行线称为测地圆，其半径等于u.

[高涅-波恩涅公式] 设G为曲面S上一个单连通区域，G的边界C是一条逐段光滑并无自交点的闭曲线，其运行的方向是使G总是在它的左侧.

图 7.29

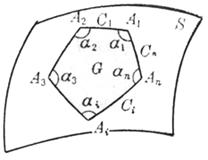
设表示曲线C上任一点的测地曲率，为曲面面积元素，分别为C的角点的内角（图），则在G上的二重积分

这称为高斯-波恩涅公式.特别

1、如果C是一条正则曲线（即无角点），这时，则

2、如果C是由n条测地线组成的测地多角形，这时（因=0）

当时，C为三条测地线组成的测地三角形，这时

因次，的曲面上的测地三角形三内角之和大于；的曲面上测地三角形三内角之和小于；的曲面上测地三角形三内角之和等于.