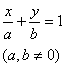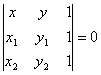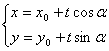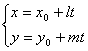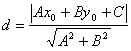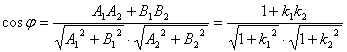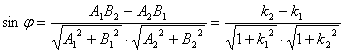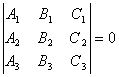§3 平面上的直线
一、平面上直线的方程与图形
|
方 程 与 图 形 |
说 明 |
||||||
|
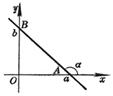
[斜截式] |
|
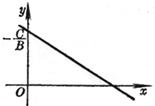
k为斜率.若直线与x轴的交角为a,则 b为纵截距
|
|||||
|
|
|||||||
|
[截距式]
|
|
a,b分别为x轴,y轴上的截距. 该直线通过A(a, 0)和B(0, b)两点. 与x轴的交角
或 |
|||||
|
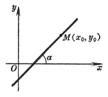
[点斜式] |
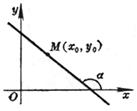
k为斜率 该直线通过点M(x0, y0),与x轴的交角
|
||||||
|
方 程 |
与 图 形 |
说 明 |
|||||
|
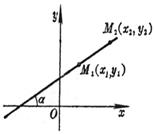
[两点式]
或
|
|
该直线通过M1(x1, y1)与M2(x2, y2)两点, 与x轴的交角
|
|||||
|
[一般式]
|
|
斜率 纵截距 [注]一般方程可根据需要化成上面四种形式
|
|||||
|
[参数式]
或 (-∞< t <∞) |
|
斜率 该直线通过点M(x0, y0)与x轴的交角为a
|
|||||
|
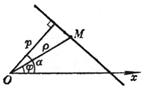
[极坐标式] |
|
O为极点,Ox为极轴,p为极点到该直线的距离.a为极轴与从极点引到直线的垂线之间的夹角(逆时针方向为正),j为该直线上任一点M的极角,r为M点的矢径
|
|||||
|
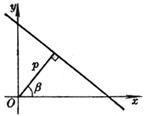
[法线式]
|
p为法线长(原点O到直线的垂线长),b为法线与x轴的交角,p, b称为直线的位置参数. [注]直线一般式可化为法线式 式中 |
||||||
|
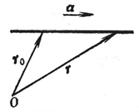
[矢量式]
|
该直线通过矢径r0的终点,且与已知矢量a平行
|
||||||
|
方 程 |
与 图 形 |
说 明 |
|||||
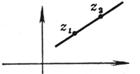
|
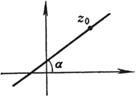
[复数式]
(a)
(b)
|
|
(a) 直线通过点z0,并与x轴的交角为a
(b) 直线通过z1,z2两点(t为实参数) |
|||||
二、平面上点与直线的相互关系
|
方 程 与 图 形 |
计 算 公 式 与 说 明 |
|
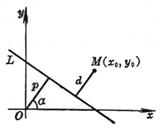
[点线的距离] 法线式 一般式
|
d法=
式中d为点M(x0, y0)到直线L的距离 |
|
[二直线的夹角] L1 A1x + B1y + C1 = 0 斜率为k1 L2 A2x + B2y + C2= 0 斜率为k2
|
特别, 当 当 当A1A2+B1B2 = 0 (或1 + k1k2 = 0)时,L1⊥L2
|
|
方 程 与 图 形 |
计 算 公 式 与 说 明 |
|
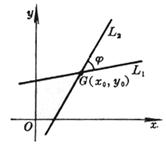
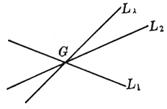
[直线束×三直线共点的条件] Ll (A1x + B1y + C1) + l(A2x + B2y + C2) = 0, (l为参数,-¥<l< ¥)
|
对l的一个确定值,Ll表示一条通过二直线(L1和L2)的交点G的直线,当l取一切值时,Ll所表示的通过G的直线的全体称为直线束,G称为直线束的顶点(或中心). 设L3为A3x + B3y + C3 = 0,则三条直线L1, L2, L3共点的条件为行列式 如果二直线方程以法线式给定,则|l|为直线Ll上任一点到二给定直线之间的距离之比,对应与 l = 1和 l = -1的直线为给定二直线夹角的平分线
|