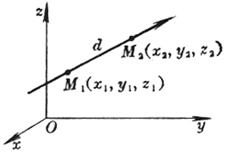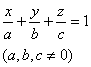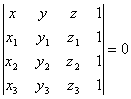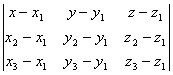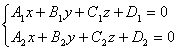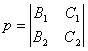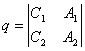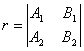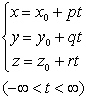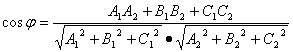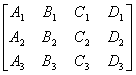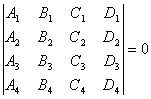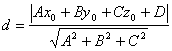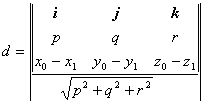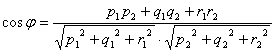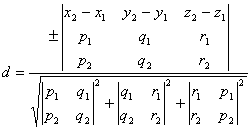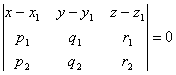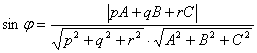§4  空间中的直线与平面

 

一、         直线的方向

 

名  称  与  说  明

图  形

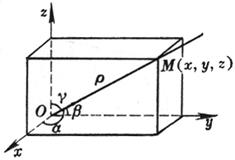
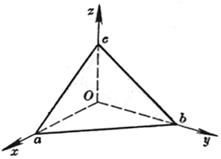
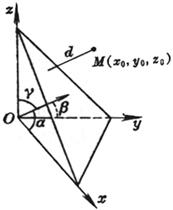
[方向角]

       通过原点O的直线OM与三条坐标轴的夹角a, b, g 称为该直线的方向角(OM的方向为离开原点O的方向)：

       a =∠MOx，b =∠MOy，g =∠MOz

[方向余弦]

       直线的方向角的余弦称为方向余弦：

       ，，

式中      ，l2 + m2 + n2 = 1

 

 

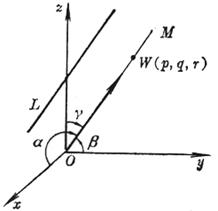
[方向数]

       通过原点且平行于直线L的直线OM上任意一点W的坐标(p, q, r)称为直线L的方向数，而

       为直线OM的方向余弦

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

      名  称  与  说  明

            图  形

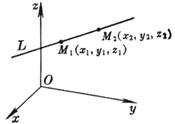
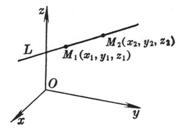
[过两点的直线的方向余弦]

，，

式中      

这时直线的正向为M1(x1, y1, z1)到M2(x2, y2, z2)的方向.

 

 

 

二、         平面的方程

 

方  程  与  图  形

说  明

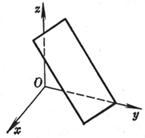
[截距式]

 

      

  

   a, b, c分别称为平面在三条坐标轴上的截距

 

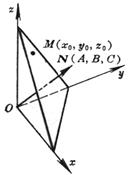
[点法式]

(A, B, C不同时等于零)

              

      

 

 

    平面通过点M(x0, y0, z0)，且法线N的方向数为A, B, C

 

 

 

 

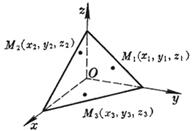
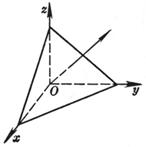
[三点式]   

 

 

      

 

 

 

 

   平面通过三点:

         M1(x1, y1, z1)

         M2(x2, y2, z2)

         M3(x3, y3, z3)

 

 或

   =0

 

 

 

 

               方  程

与  图  形

                说  明

 

 

[一般式]

  Ax + By + Cz + D = 0

  (A, B, C为该平面的法线的方向数，且不同时等于零)                   

当D=0时，平面通过原点

       当A=0时(或B=0，或C=0)时，平面与x轴(或y轴，或z轴)平行

       当A=B=0时(或A=C=0，或B=C=0)时，平面与Oxy平面(或Ozx，或Oyz)平行

[法线式]

 

  (a, b, g为平面的法线的方向角，p³0为法线长即原点到平面的距离)

                   

 

       平面的一般式可化为法线式       ，式中称为平面的法化因子，当D< 0时取正号；D>0时取负号

 

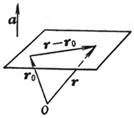
[矢量式]

(r -r0)× a = 0

 

      

 

  平面 通过矢径r0的终点，且与已知矢量a垂直，r为平面上任意一点的矢径

 

 

三、         直线的方程

 

方  程  与  图  形

说  明

[一般式(或交面式)]

L    

               

          把直线L作为两个平面的交线，它的方向数为

[对称式(或参数式)]

或        

 

 

 

    直线L通过点M(x0, y0, z0)，且具有方向数p, q, r

 

 

 

 

 

 

 

 

 

           方  程  与  图  形

            说  明

[两点式]

                    

 

 

    直线L通过M1(x1, y1, z1)和M2(x2, y2, z2)两点

 

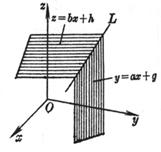
[射影式]

L    

     

  

 

   直线L是y = ax+ g 和z = bx + h两个平面的交线；通过点(0, g, h)且具有方向数1, a, b

 

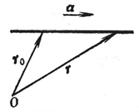
[矢量式]

  r = r0 + ta

  (-¥< t < ¥)

 

 

 

 

    直线L通过矢径r0的终点，且与已知矢量a平行，r为L上任意一点的矢径

 

 

四、         空间中点、直线、平面的相互关系

 

方  程  与  图  形

公  式  与  说  明

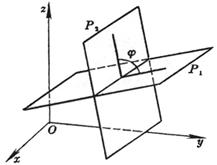
[二平面的夹角]

 P1 A1x + B1y + C1z + D1 = 0

 P2 A2x + B2y + C2z + D2 = 0

 

 

 

 

 

   

 

 

 

 

 

   

    式中就是二平面P1和P2的二面角

 

 

 

 

 

 

 

 

 

   方  程  与  图  形

             公  式  与  说  明

 

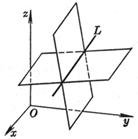
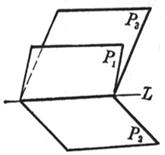
[平面束×三平面共线的条件]

Pl   (A1x+ B1y + C1z + D1) + l  (A2x + B2y + C2z + D2) = 0

  (l为参数，-¥<l< ¥)

      

 

 

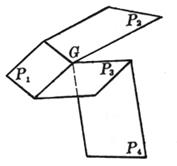
[平面把×四平面共点的条件]

Plm    (A1x + B1y + C1z + D1) + 

     l (A2x + B2y + C2z + D2) +

     m (A3x + B3y + C3z + D3)

      = 0

  (l, m为两个独立参数，

   - ¥ < l , m < ¥)

 

 

对l的一个确定值，Pl表示一个通过二平面P1和P2交

线L的平面，当l取一切值时，Pl所表示的通过L的平面的全体称为平面束，L称为束的轴.

       设P3为A3x + B3y + C3z + D3 = 0，则三个平面P1, P2, P3共线的条件为矩阵

      

的秩等于2.

      

   

 

 

 对l,m的一对确定值，Plm表示通过三平面P1, P2和P3交点G的一个平面，当l, m取一切值时，Plm       所表示的通过G的平面的全体称为平面把，G称为把的顶点.

       设P4为A4x + B4y + C4z + D4 = 0，则四个平面P1, P2, P3, P4共点的条件为行列式

                

[点面的距离]

  法线式

  xcosa + ycosb + zcosg - p = 0

一般式  Ax + By + Cz + D = 0

     

 

      

 

 

 

 

    d法 = | x0cosa + y0cosb + z0cosg - p |

      

       式中d为点M(x0,y0,z0)到平面的距离

 

    方  程  与  图  形

             公  式  与  说  明

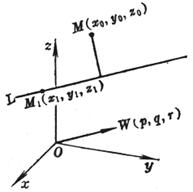
[点线的距离]

L    

   

 

 

   

式中d为点M(x0, y0, z0)到直线L的距离，i，j，k为三个坐标轴上的单位矢量，最外面的符号“|  |”表示矢量的模

 

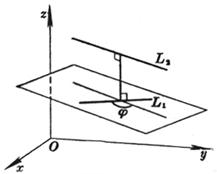
[二直线的夹角]

L1 

L2 

 

 

 

         

式中j为二直线L1和L2的夹角

 

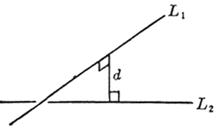
[二不平行直线的最短距离]

       L1    

       L2   

  

       所谓最短距离是指L1, L2的公共垂线与此两线交点之间的距离，式中正负号与行列式取同号.从此推出二直线共面的条件为d=0，所在平面的方程为    

             

 

 

 

 

 

 

 

 

 

 

     方  程  与  图  形

          公  式  与  说  明

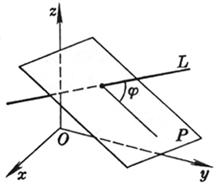
[直线与平面的夹角]

L    

P     Ax + By + Cz + D = 0

  

 

 

式中j为直线L与平面P的夹角

 

 

[直线与平面的平行与垂直条件]

 

平  行  条  件

垂  直  条  件

线与线 

面与面 

线与面 

 

    p1p2 + q1q2 + r1r2 = 0

 

       A1A2 + B1B2 + C1C2 = 0