§7 平面曲线
[曲线方程与正方向]
|
曲线方程的形式 |
曲线的正向 |
|
直角坐标系
隐 式 F(x,y) = 0 显 式 y = f(x)
参数式 (t为任意参数,s为曲线的弧长) 极坐标系 r = r(j)
|
x增加时,曲线上一点的运动方向
t或s增加时,曲线上一点的运动方向
j增加(即逆时针方向)时,曲线上一点运动方向 |
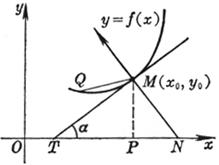
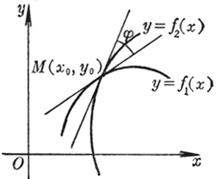
[曲线的切线与法线] 当曲线上的点Q趋于M时,割线MQ的极限位置称为曲线在点M处的切线,通过点M并垂直于切线的直线称为法线.切线的正向就是曲线在切点处的正向,法线的正向就是切线的正向按逆时针方向旋转90°而得到的方向.
[曲线的切矩、法矩、次切矩、次法矩与切线倾斜度公式]
|
|
直角坐标系 |
极坐标系 |
|
图 形 |
|
|
|
切 距 |
|
|
|
法 距 |
|
|
|
次切距 |
|
|
|
次法距 |
|
|
|
切线倾斜度 |
tan a |
|
表中![]() .对于参数表达的曲线,表中
.对于参数表达的曲线,表中
![]()
![]() .
.
[曲线的切线方程与法线方程]
|
曲线方程 |
切线方程(MT) |
法线方程(MN) |
|
F(x,y) = 0 |
|
|
|
y = f(x) |
|
|
|
|
|
|
|
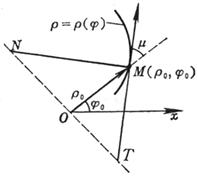
r = r(j) |
|
|
|
图 7.14 |
表中![]() 分别表示
分别表示![]() 在点
在点![]() 的值,
的值,![]() 同前.
同前.
[曲线的夹角] 两条相交于点![]() 的曲线
的曲线![]() 和
和![]() 在交点的切线斜率分别为
在交点的切线斜率分别为![]() 和
和![]() ,其夹角j称为两条曲线的夹角(图7.14),且
,其夹角j称为两条曲线的夹角(图7.14),且
![]()
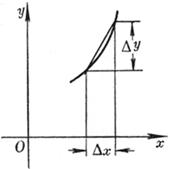
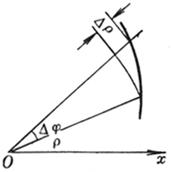
[弧的微分]
|
曲线方程与图形 |
弧的微分ds |
||
|
y =
f(x) r = r(j) |
|
|
|
|
图 7.15 |
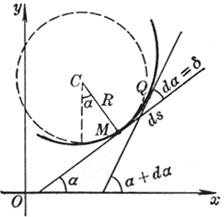
[曲率、曲率半径、曲率圆(或密切圆)与曲率中心的定义]
曲线上两点M和Q的切线正向的夹角d与弧长![]() 之比,当Q趋于M时的极限,即
之比,当Q趋于M时的极限,即

称为曲线在点M的曲率,也就是切线的方向角对于弧长的转动率.当k>0时,表明曲线凹向朝法线的正向;当k<0时, 表明曲线凹向朝法线的负向(图7.15).
![]()
称为曲线在点M的曲率半径.在曲线凹向的法线上截![]() ,则称C为曲线在点M的曲率中心,以C为圆心,R为半径的圆称为曲线在点M的曲率圆,又称为密切圆.C点的坐标为
,则称C为曲线在点M的曲率中心,以C为圆心,R为半径的圆称为曲线在点M的曲率圆,又称为密切圆.C点的坐标为
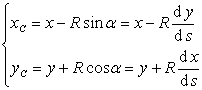
[曲率半径与曲率中心坐标的计算公式] 设R为曲率半径,(![]() )为曲率中心的坐标,则有
)为曲率中心的坐标,则有
1°曲线方程为F(x,y) = 0时



2° 曲线方程为y = f (x)时
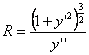
![]()
![]()
3° 曲线方程为![]() 时
时
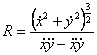
![]()
![]()
4° 曲线方程为![]() 时
时
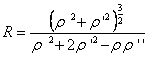
![]()
![]()
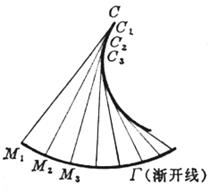
[等距线、渐屈线、渐开线与包络线]
|
定 义 与 图 形 |
方程与说明(G : y = f (x)) |
|
等距线 曲线G 上的每点沿G 在该点法线的一定方向(正负两个方向)移动等距离a得到新的点,这些点的轨迹
渐屈线 曲线G 上的每点的曲率中心的轨迹C称为曲线G 的渐屈线,也称为曲线G 的法包线(即曲线的法线的包络线)
渐开线 曲线G 对它的渐屈线C而言,就是渐开线(或称渐伸线)
定 义 与 图 形 |
式中正负号上边对应于 如果G 为参数式方程 则有以t为参数的方程
这个方程是以x为参数的参数方程.其他形式表达的曲线G 的渐屈线的方程参见曲率中心的公式
设C的方程为y = f (x),则G Y = Y (x)或 它是微分方程组 的解,式中 方程与说明(G : y = f (x)) |
|
渐开线的性质 1° 渐开线G 上任一点的法线与曲线C相切 2° 渐开线上两点 3° 渐开线的等距线是和它一样的渐开线,它们仅仅是起点不同.
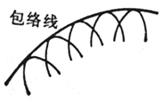
包络线 与曲线族所有曲线都相切的曲线称为该曲线族的包络线 |
其他形式表达的曲线的渐开线方程可由表示曲率中心的坐标的微分方程组而解出
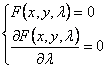
隐式 显式 参数式 消去l得到不同形式的方程,它们所表示的曲线称为判别曲线,包含包络线与由奇点组成的曲线(例如,曲线族F(x,y,l)=0上的点满足
|
|
(b) |
|
(a) |
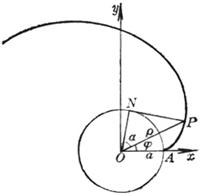
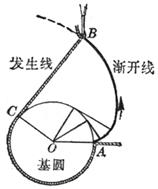
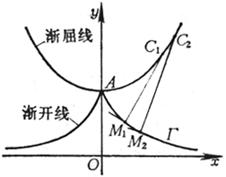
例 在圆盘周围绕上一根不会伸缩的细线,线端栓一支铅笔,拉紧线端A逐渐拉开,铅笔尖在纸上画出来的曲线就是圆的渐开线.这个圆称为渐开线的基圆.细线称为渐开线的发生线(图7.16(a) ).
现在来寻求渐开线的方程.设基圆的圆心是O,半径是a.开始画时,发生线的外端在A点,取OA为x轴(极轴),如图7.16(b).再设线外端P的坐标为(x,y)或(r,j),因为发生线原来对着圆心角为a +j (a =ÐPON,在齿轮设计中,通称为压力角)的一段弧![]() ,展开成为切线NP,所以切线NP的长是a(a + j ),从直角三角形ONP得:OP=
,展开成为切线NP,所以切线NP的长是a(a + j ),从直角三角形ONP得:OP=![]() ,又因
,又因![]() = a + j,由此得到圆的渐开线方程
= a + j,由此得到圆的渐开线方程
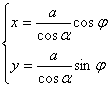
式中a是依赖于极角j的,这个关系决定于![]() ,把上式写为极坐标方程
,把上式写为极坐标方程
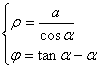 (a 单位为弧度)
(a 单位为弧度)
设t = a + j,可得直角坐标参数方程
![]() (a 为基圆半径)
(a 为基圆半径)
[雪列-弗莱纳公式]
![]()
式中t和n分别为曲线的切线和法线的单位矢量,s为弧长,R为曲率半径.
[基本定理与自然方程] 在闭区间[a,b]上给定一个连续函数k(s),则除了在平面上的位置差别外,唯一地存在一条平面曲线,以s为弧长,k(s)为曲率.k = k(s)称为曲线的自然方程.
[两条平面曲线构成n阶接触的概念与条件]
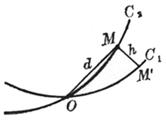
|
图 7.17 |
设两条曲线C1和C2有一共同点O,在C2上取一点M,从M到C1的距离设为h,以d表示M到O的距离(图7.17),如果
![]()
则称两条曲线C1与C2在点O构成n阶接触.
检验两条平面曲线构成n阶接触的准则:
1° 设曲线C1的方程为F(x,y)=0,曲线C2的方程为x = x(t),y = y(t),并设在点t = t0(即O(x0,y0))处![]() ,则两条曲线C1与C2在点O构成n阶接触的充分必要条件是:
,则两条曲线C1与C2在点O构成n阶接触的充分必要条件是:
![]()
式中![]() ,
,![]() 表示j(t)n阶导数.
表示j(t)n阶导数.
从此还可推出下面的检验准则:
2° 假定C1:F(x, y) = 0是一条代数曲线(即F(x, y)是关于x和y的多项式),C2在原点(0,0) 的展开式为
![]()
则![]() 和
和![]() 在原点构成
在原点构成![]() 阶接触的充分必要条件是:把
阶接触的充分必要条件是:把![]() 的展开式代进
的展开式代进![]() 后,关于
后,关于![]() 的乘幂
的乘幂![]() ,
,![]() 的系数都等于零.
的系数都等于零.
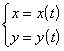
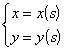
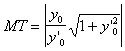
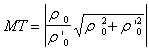
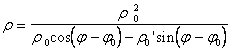
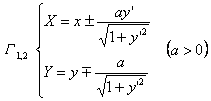
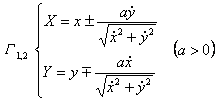


 (
( (
( (
(