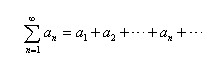2

2. 同号级数收敛判别法

设

(1)

(2)

为两个同号级数（即每一项符号相同的级数，当都是正号时，称为正项级数），这类级数的收敛判别法见下表.

名称		条件	级数的收敛性
名称		条件	收敛	发散
比较判别法	I	当n>N时， 0≤a_n≤b_n	若级数(2)收敛，则级数(1)收敛	若级数(1)发散，则级数(2)发散
	II	(0≤K≤+∞) (b_n≠0)	当K<+时，若级数(2)收敛，则级数(1)收敛	当K>0时，若级数(2)发散，则级数(1)发散
	III	当n>N时， ≤ (a_n≠0,b_n≠0)	若级数(2)收敛，则级数(1)收敛	若级数(1)发散，则级数(2)发散
	IV	当n→∞时， a_n～b_n	级数(1)和(2)同时收敛	级数(1)和(2)同时发散
	V	a_n=O^*()	当p>1时	当p≤1时
达兰贝尔判别法		a_n>0(n=1,2,…)=q	当q<1时	当q>1时
柯西判别法		a_n≥0(n=1,2,…)	当q<1时	当q>1时
拉阿伯判别法		a_n>0(n=1,2,…) =p	当p>1时	当p<1时
高斯判别法		a_n>0(n=1,2,…) 其中有界： ≤L,>0	当λ>1时，或者当λ=1，而μ>1时	当λ<1时，或者当λ=1，而μ≤1时
柯西积分判别法		f(x) (x≥1) 为非负不增函数	与同时收敛	与同时发散
对数判别法		a_n>0(n=1,2,…) 设	当n>N()， >0时，	当n≥N()， >0时，