|
|
|
The Ackermann function is the simplest example of a well-defined Total Function which is
Computable but not Primitive Recursive, providing a
counterexample to the belief in the early 1900s that every Computable Function was also Primitive
Recursive (Dötzel 1991). It grows faster than an exponential function, or even a multiple
exponential function. The Ackermann function ![]() is defined by
is defined by
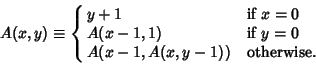 |
(1) |
| (2) | |||
| (3) | |||
| (4) | |||
| (5) | |||
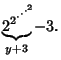 |
(6) |
| (7) |
| (8) |
Buck (1963) defines a related function using the same fundamental Recurrence Relation (with arguments
flipped from Buck's convention)
| (9) |
| (10) | |||
| (11) | |||
| (12) | |||
| (13) |
| (14) | |||
| (15) | |||
| (16) | |||
| (17) |
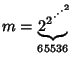 , a
truly huge number!
, a
truly huge number!
See also Ackermann Number, Computable Function, Goodstein Sequence, Power Tower, Primitive Recursive Function, TAK Function, Total Function
References
Buck, R. C. ``Mathematical Induction and Recursive Definitions.'' Amer. Math. Monthly 70, 128-135, 1963.
Dötzel, G. ``A Function to End All Functions.'' Algorithm: Recreational Programming 2.4, 16-17, 1991.
Kleene, S. C. Introduction to Metamathematics. New York: Elsevier, 1971.
Péter, R. Rekursive Funktionen. Budapest: Akad. Kiado, 1951.
Reingold, E. H. and Shen, X. ``More Nearly Optimal Algorithms for Unbounded Searching, Part I: The Finite Case.''
SIAM J. Comput. 20, 156-183, 1991.
Rose, H. E. Subrecursion, Functions, and Hierarchies. New York: Clarendon Press, 1988.
Sloane, N. J. A. Sequence
A001695/M2352
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Smith, H. J. ``Ackermann's Function.'' http://pweb.netcom.com/~hjsmith/Ackerman.html.
Spencer, J. ``Large Numbers and Unprovable Theorems.'' Amer. Math. Monthly 90, 669-675, 1983.
Tarjan, R. E. Data Structures and Network Algorithms. Philadelphia PA: SIAM, 1983.
Vardi, I. Computational Recreations in Mathematica. Redwood City, CA: Addison-Wesley, pp. 11, 227, and 232, 1991.
|
|
|
© 1996-9 Eric W. Weisstein