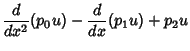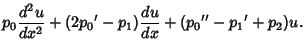Adjoint Operator

Given a Second-Order Ordinary Differential Equation

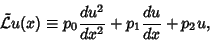$\begin{displaymath} {\tilde {\mathcal L}} u(x) \equiv p_0 {du^2\over dx^2} +p_1 {du \over dx} +p_2 u, \end{displaymath}$

(1)

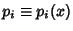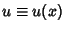where $p_i \equiv p_i(x)$ and $u\equiv u(x)$ , the adjoint operator 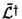${\tilde {\mathcal L}}^\dagger$ is defined by

$\displaystyle {\tilde {\mathcal L}}^\dagger u$	$\textstyle \equiv$	$\displaystyle {d\over dx^2} (p_0 u)-{d \over dx} (p_1 u)+p_2 u$
	$\textstyle =$	$\displaystyle p_0 {d^2 u\over dx^2} +(2{p_0}'-p_1) {du\over dx} + ({p_0}''-{p_1}'+p_2)u.$
			(2)

Write the two Linearly Independent solutions as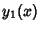

and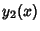

. Then the adjoint operator can also be written

$\begin{displaymath} {\tilde {\mathcal L}}^\dagger u = \int (y_2 {\tilde {\mathca... ...\,dx = {\left[{{p_1\over p_0} ({y_1}'y_2-y_1{y_2}')}\right]}. \end{displaymath}$

(3)