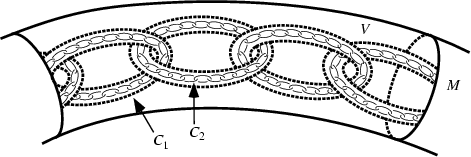
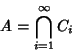Construct a chain 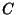 of
of 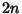 components in a solid Torus
components in a solid Torus 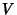 . Now form a chain
. Now form a chain 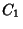 of
of 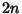 solid tori in
solid tori in 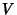 ,
where
,
where
via inclusion. In each component of 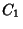 , construct a smaller chain of solid tori embedded in that component.
Denote the union of these smaller solid tori
, construct a smaller chain of solid tori embedded in that component.
Denote the union of these smaller solid tori 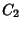 . Continue this process a countable number of times, then the
intersection
. Continue this process a countable number of times, then the
intersection
which is a nonempty compact Subset of 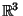 is called Antoine's necklace. Antoine's necklace is Homeomorphic
with the Cantor Set.
is called Antoine's necklace. Antoine's necklace is Homeomorphic
with the Cantor Set.
See also Alexander's Horned Sphere, Necklace
References
Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, pp. 73-74, 1976.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() of
of ![]() components in a solid Torus
components in a solid Torus ![]() . Now form a chain
. Now form a chain ![]() of
of ![]() solid tori in
solid tori in ![]() ,
where
,
where