|
|
|
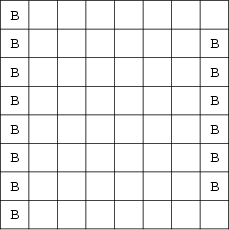
Find the maximum number of bishops ![]() which can be placed on an
which can be placed on an ![]() Chessboard such that no two attack each
other. The answer is
Chessboard such that no two attack each
other. The answer is ![]() (Dudeney 1970, Madachy 1979), giving the sequence 2, 4, 6, 8, ... (the Even
Numbers) for
(Dudeney 1970, Madachy 1979), giving the sequence 2, 4, 6, 8, ... (the Even
Numbers) for ![]() , 3, .... One maximal solution for
, 3, .... One maximal solution for ![]() is illustrated above. The number of distinct
maximal arrangements of bishops for
is illustrated above. The number of distinct
maximal arrangements of bishops for ![]() , 2, ... are 1, 4, 26, 260, 3368, ... (Sloane's A002465). The number of
rotationally and reflectively distinct solutions on an
, 2, ... are 1, 4, 26, 260, 3368, ... (Sloane's A002465). The number of
rotationally and reflectively distinct solutions on an ![]() board for
board for ![]() is
is
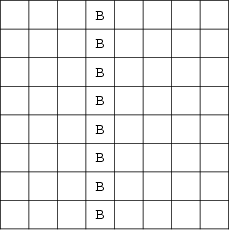
The minimum number of bishops needed to occupy or attack all squares on an ![]() Chessboard is
Chessboard is ![]() , arranged
as illustrated above.
, arranged
as illustrated above.
See also Chess, Kings Problem, Knights Problem, Queens Problem, Rooks Problem
References
Ahrens, W. Mathematische Unterhaltungen und Spiele, Vol. 1, 3rd ed. Leipzig, Germany: Teubner, p. 271, 1921.
Dudeney, H. E. ``Bishops--Unguarded'' and ``Bishops--Guarded.'' §297 and 298 in
Amusements in Mathematics. New York: Dover, pp. 88-89, 1970.
Guy, R. K. ``The
Madachy, J. Madachy's Mathematical Recreations. New York: Dover, pp. 36-46, 1979.
Pickover, C. A. Keys to Infinity. New York: Wiley, pp. 74-75, 1995.
Sloane, N. J. A. Sequences
A002465/M3616
and A005418/M0771
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
![]() Queens Problem.'' §C18 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 133-135, 1994.
Queens Problem.'' §C18 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 133-135, 1994.
|
|
|
© 1996-9 Eric W. Weisstein