|
|
|
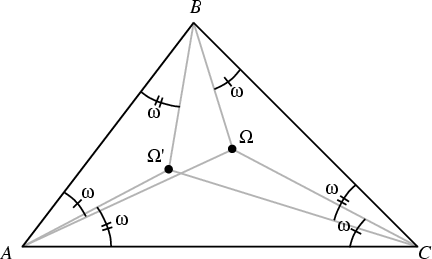
The first Brocard point is the interior point ![]() (or
(or ![]() or
or ![]() ) of a Triangle for which the
Angles
) of a Triangle for which the
Angles
![]() ,
,
![]() , and
, and
![]() are equal. The second Brocard point is
the interior point
are equal. The second Brocard point is
the interior point ![]() (or
(or ![]() or
or ![]() ) for which the Angles
) for which the Angles
![]() ,
,
![]() , and
, and
![]() are equal. The Angles in both cases are equal to the
Brocard Angle
are equal. The Angles in both cases are equal to the
Brocard Angle ![]() ,
,
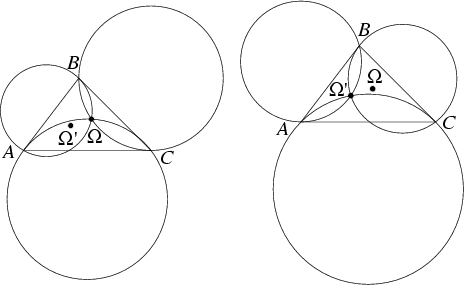
Let ![]() be the Circle which passes through the vertices
be the Circle which passes through the vertices ![]() and
and ![]() and is Tangent to the line
and is Tangent to the line ![]() at
at ![]() ,
and similarly for
,
and similarly for ![]() and
and ![]() . Then the Circles
. Then the Circles ![]() ,
, ![]() , and
, and ![]() intersect in the
first Brocard point
intersect in the
first Brocard point ![]() . Similarly, let
. Similarly, let ![]() be the Circle which passes through the vertices
be the Circle which passes through the vertices ![]() and
and ![]() and
is Tangent to the line
and
is Tangent to the line ![]() at
at ![]() , and similarly for
, and similarly for ![]() and
and ![]() . Then the Circles
. Then the Circles
![]() ,
, ![]() , and
, and ![]() intersect in the second Brocard points
intersect in the second Brocard points ![]() (Johnson 1929, pp. 264-265).
(Johnson 1929, pp. 264-265).
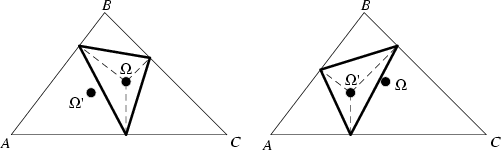
The Pedal Triangles of ![]() and
and ![]() are congruent, and Similar to the
Triangle
are congruent, and Similar to the
Triangle ![]() (Johnson 1929, p. 269). Lengths involving the Brocard points include
(Johnson 1929, p. 269). Lengths involving the Brocard points include
| (1) |
| (2) |
Brocard's third point is related to a given Triangle by the Triangle Center Function
| (3) |
See also Brocard Angle, Brocard Midpoint, Equi-Brocard Center, Yff Points
References
Casey, J. A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing
an Account of Its Most Recent Extensions, with Numerous Examples, 2nd ed., rev. enl. Dublin: Hodges, Figgis, & Co., p. 66, 1893.
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA:
Houghton Mifflin, pp. 263-286, 1929.
Kimberling, C. ``Central Points and Central Lines in the Plane of a Triangle.'' Math. Mag. 67, 163-187, 1994.
Stroeker, R. J. ``Brocard Points, Circulant Matrices, and Descartes' Folium.'' Math. Mag. 61, 172-187, 1988.
|
|
|
© 1996-9 Eric W. Weisstein