|
|
|
A modified set of Chebyshev Polynomials defined by a slightly different Generating Function.
Used to develop four-dimensional Spherical Harmonics in
angular momentum ![]() theory. They are also a special case of the Ultraspherical Polynomial with
theory. They are also a special case of the Ultraspherical Polynomial with ![]() .
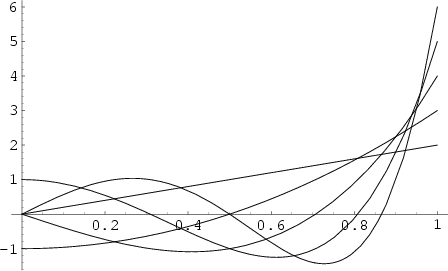
The Chebyshev polynomials of the second kind
.
The Chebyshev polynomials of the second kind ![]() are illustrated above for
are illustrated above for ![]() and
and ![]() , 2, ..., 5.
, 2, ..., 5.
The defining Generating Function of the Chebyshev polynomials of the second kind is
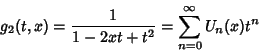 |
(1) |
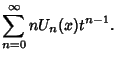 |
(2) |
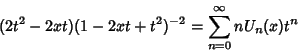 |
(3) |
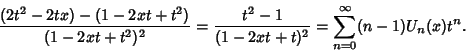 |
(4) |
| (5) |
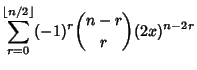 |
|||
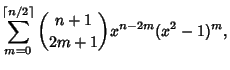 |
(6) |
 |
(7) |
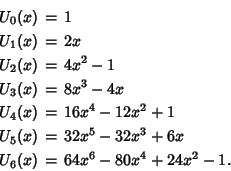
Letting
![]() allows the Chebyshev polynomials of the second kind to be written as
allows the Chebyshev polynomials of the second kind to be written as
| (8) |
| (9) |
| (10) |
See also Chebyshev Approximation Formula, Chebyshev Polynomial of the First Kind, Ultraspherical Polynomial
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Orthogonal Polynomials.'' Ch. 22 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 771-802, 1972.
Arfken, G. ``Chebyshev (Tschebyscheff) Polynomials'' and ``Chebyshev Polynomials--Numerical Applications.''
§13.3 and 13.4 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 731-748, 1985.
Rivlin, T. J. Chebyshev Polynomials. New York: Wiley, 1990.
Spanier, J. and Oldham, K. B. ``The Chebyshev Polynomials
![]() and
and ![]() .''
Ch. 22 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 193-207, 1987.
.''
Ch. 22 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 193-207, 1987.
|
|
|
© 1996-9 Eric W. Weisstein