Closure

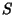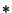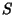A Set $S$ and a Binary Operator $*$ are said to exhibit closure if applying the Binary Operator to two elements $S$ returns a value which is itself a member of $S$.

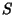The term ``closure'' is also used to refer to a ``closed'' version of a given set. The closure of a Set can be defined in several equivalent ways, including

1. The Set plus its Limit Points, also called ``boundary'' points, the union of which is also called the ``frontier,''

2. The unique smallest Closed Set containing the given Set,

3. The Complement of the interior of the Complement of the set,

4. The collection of all points such that every Neighborhood of them intersects the original Set in a nonempty Set.

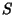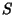In topologies where the T2-Separation Axiom is assumed, the closure of a finite Set $S$ is $S$ itself.

See also Binary Operator, Existential Closure, Reflexive Closure, Tight Closure, Transitive Closure