|
|
|
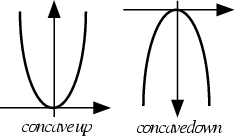
A function whose value at the Midpoint of every Interval in its Domain does not exceed the
Average of its values at the ends of the Interval. In other words, a function ![]() is convex on an
Interval
is convex on an
Interval ![]() if for any two points
if for any two points ![]() and
and ![]() in
in ![]() ,
,
See also Concave Function, Logarithmically Convex Function
References
Eggleton, R. B. and Guy, R. K. ``Catalan Strikes Again! How Likely is a Function to be Convex?''
Math. Mag. 61, 211-219, 1988.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, p. 1100, 1980.