Cyclic Polygon

A cyclic polygon is a Polygon with Vertices upon which a Circle can be Circumscribed. Since every Triangle has a Circumcircle, every Triangle is cyclic. It is conjectured that for a cyclic polygon of $2m+1$ sides, $16K^2$ (where $K$ is the Area) satisfies a Monic Polynomial of degree $\Delta_m$, where

$$\Delta_m \equiv \sum_{k=0}^{m-1} (m-k){2m+1\choose k}$$ (1)

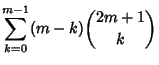$$= {1\over 2}\left[{(2m+1){2m\choose m}-2^{2m}}\right]$$ (2)

(Robbins 1995). It is also conjectured that a cyclic polygon with $2m+2$ sides satisfies one of two Polynomials of degree $\Delta_m$. The first few values of $\Delta_m$ are 1, 7, 38, 187, 874, ... (Sloane's A000531).

For Triangles $(n=3=2\cdot 1+1)$, the Polynomial is Heron's Formula, which may be written

$$16K^2=2a^2b^2+2a^2c^2+2b^2c^2-a^4-b^4-c^4,$$ (3)

and which is of order $\Delta_1=1$ in $16K^2$. For a Cyclic Quadrilateral, the Polynomial is Brahmagupta's Formula, which may be written

$$16K^2 = -a^4 + 2a^2b^2 - b^4 + 2a^2c^2 + 2b^2c^2 - c^4$$

$$\phantom{=} + 8abcd + 2a^2d^2 + 2b^2d^2 + 2c^2d^2 - d^4,$$ (4)

which is of order $\Delta_1=1$ in $16K^2$. Robbins (1995) gives the corresponding Formulas for the Cyclic Pentagon and Cyclic Hexagon.

See also Concyclic, Cyclic Hexagon, Cyclic Pentagon, Cyclic Quadrangle, Cyclic Quadrilateral

References

Robbins, D. P. ``Areas of Polygons Inscribed in a Circle.'' Discr. Comput. Geom. 12, 223-236, 1994.

Robbins, D. P. ``Areas of Polygons Inscribed in a Circle.'' Amer. Math. Monthly 102, 523-530, 1995.

Sloane, N. J. A. Sequence A000531 in ``The On-Line Version of the Encyclopedia of Integer Sequences.'' http://www.research.att.com/~njas/sequences/eisonline.html.