|
|
|
Nonintersecting curves which can be iterated to yield more and more sinuosity. They can be constructed by taking a path
around a set of dots, representing a left turn by 1 and a right turn by 0. The first-order curve is then denoted 1. For
higher order curves, add a 1 to the end, then copy the string of digits preceding it to the end but switching its center
digit. For example, the second-order curve is generated as follows: (1)1 ![]() (1)1(0)
(1)1(0) ![]() 110, and the third as: (110)1
110, and the third as: (110)1
![]() (110)1(100)
(110)1(100) ![]() 1101100. Continuing gives 110110011100100... (Sloane's A014577). The Octal representation
sequence is 1, 6, 154, 66344, ...(Sloane's A003460). The dragon curves of orders 1 to 9 are illustrated below.
1101100. Continuing gives 110110011100100... (Sloane's A014577). The Octal representation
sequence is 1, 6, 154, 66344, ...(Sloane's A003460). The dragon curves of orders 1 to 9 are illustrated below.
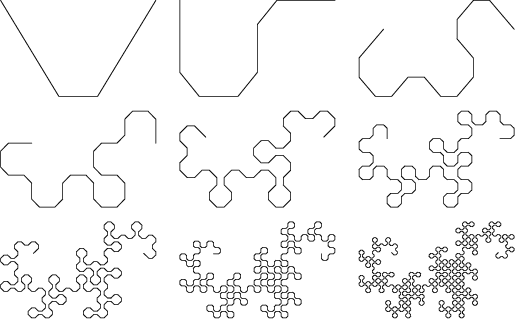
This procedure is equivalent to drawing a Right Angle and subsequently replacing each Right Angle with another smaller Right Angle (Gardner 1978). In fact, the dragon curve can be written as a Lindenmayer System with initial string "FX", String Rewriting rules "X" -> "X+YF+", "Y" -> "-FX-Y", and angle 90°.
See also Lindenmayer System, Peano Curve
References
Dickau, R. M. ``Two-Dimensional L-Systems.''
http://forum.swarthmore.edu/advanced/robertd/lsys2d.html.
Dixon, R. Mathographics. New York: Dover, pp. 180-181, 1991.
Dubrovsky, V. ``Nesting Puzzles, Part I: Moving Oriental Towers.'' Quantum 6, 53-57 (Jan.) and
49-51 (Feb.), 1996.
Dubrovsky, V. ``Nesting Puzzles, Part II: Chinese Rings Produce a Chinese Monster.''
Quantum 6, 61-65 (Mar.) and
58-59 (Apr.), 1996.
Gardner, M. Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleight-of-Mind from Scientific American.
New York: Vintage, pp. 207-209 and 215-220, 1978.
Lauwerier, H. Fractals: Endlessly Repeated Geometric Figures. Princeton, NJ: Princeton University Press,
pp. 48-53, 1991.
Peitgen, H.-O. and Saupe, D. (Eds.). The Science of Fractal Images. New York: Springer-Verlag, p. 284, 1988.
Sloane, N. J. A. Sequences
A014577 and
A003460/M4300
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Vasilyev, N. and Gutenmacher, V. ``Dragon Curves.'' Quantum 6, 5-10, 1995.
|
|
|
© 1996-9 Eric W. Weisstein