Euler Formula

The Euler formula states

$$e^{ix} = \cos x+i \sin x,$$ (1)

where i is the Imaginary Number. Note that the Euler Polyhedral Formula is sometimes also called the Euler formula, as is the Euler Curvature Formula. The equivalent expression

$$ix=\ln(\cos x+i\sin x)$$ (2)

had previously been published by Cotes (1714). The special case of the formula with $x=\pi$ gives the beautiful identity

$$e^{i\pi}+1=0,$$ (3)

an equation connecting the fundamental numbers i, Pi, e, 1, and 0 (Zero).

The Euler formula can be demonstrated using a series expansion

$$e^{ix} = \sum_{n=0}^\infty {(ix)^n\over n!}$$

$$= \sum_{n=0}^\infty{(-1)^nx^{2n}\over (2n)!} +i \sum_{n=1}^\infty {(-1)^{n-1}x^{2n-1}\over (2n-1)!}$$

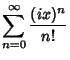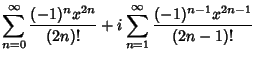$$= \cos x+i \sin x.$$ (4)

It can also be proven using a Complex integral. Let

$$z \equiv \cos \theta +i\sin \theta$$ (5)

$$dz = (-\sin \theta +i\cos \theta )\,d\theta = i(\cos \theta +i\sin \theta )\,d\theta = iz\,d\theta$$ (6)

$$\int {dz\over z} = \int i\,d\theta$$ (7)

$$\ln z = i\theta,$$ (8)

so

$$z = e^{i\theta} \equiv \cos \theta +i\sin \theta.$$ (9)

See also de Moivre's Identity, Euler Polyhedral Formula

References

Castellanos, D. ``The Ubiquitous Pi. Part I.'' Math. Mag. 61, 67-98, 1988.

Conway, J. H. and Guy, R. K. ``Euler's Wonderful Relation.'' The Book of Numbers. New York: Springer-Verlag, pp. 254-256, 1996.

Cotes, R. Philosophical Transactions 29, 32, 1714.

Euler, L. Miscellanea Berolinensia 7, 179, 1743.

Euler, L. Introductio in Analysin Infinitorum, Vol. 1. Lausanne, p. 104, 1748.