|
|
|
Arises in the testing of whether two observed samples have the same Variance. Let ![]() and
and ![]() be
independent variates distributed as Chi-Squared with
be
independent variates distributed as Chi-Squared with ![]() and
and ![]() Degrees of
Freedom. Define a statistic
Degrees of
Freedom. Define a statistic ![]() as the ratio of the dispersions of the two distributions
as the ratio of the dispersions of the two distributions
| (1) |
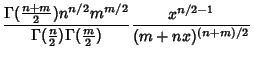 |
(2) | ||
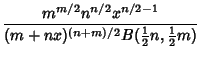 |
(3) | ||
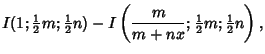 |
(4) |
| (5) | |||
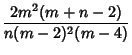 |
(6) | ||
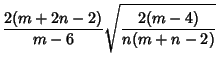 |
(7) | ||
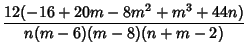 |
|||
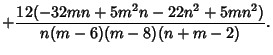 |
(8) |
The noncentral ![]() -distribution is given by
-distribution is given by
![$\displaystyle \times {\Gamma({\textstyle{1\over 2}}n_1)\Gamma(1+{\textstyle{1\o...
...ver 2}}n_1, {\textstyle{1\over 2}}n_2)\Gamma[{\textstyle{1\over 2}}(n_1+n_2)]},$](f_29.gif) |
(9) |
See also Beta Function, Gamma Function, Regularized Beta Function, Snedecor's F-Distribution
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 946-949, 1972.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T.
``Incomplete Beta Function, Student's Distribution, F-Distribution, Cumulative Binomial Distribution.'' §6.2 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge
University Press, pp. 219-223, 1992.
Spiegel, M. R. Theory and Problems of Probability and Statistics.
New York: McGraw-Hill, pp. 117-118, 1992.
|
|
|
© 1996-9 Eric W. Weisstein