On the surface of a Sphere, attempt Separation of Variables in Spherical Coordinates by writing
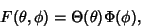 |
(1) |
then the Helmholtz Differential Equation becomes
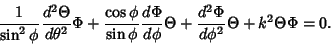 |
(2) |
Dividing both sides by 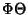 ,
,
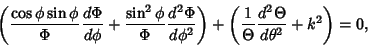 |
(3) |
which can now be separated by writing
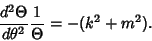 |
(4) |
The solution to this equation must be periodic, so 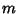 must be an Integer. The solution may then be defined either as
a Complex function
must be an Integer. The solution may then be defined either as
a Complex function
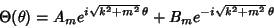 |
(5) |
for 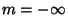 , ...,
, ..., 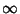 , or as a sum of Real sine and cosine functions
, or as a sum of Real sine and cosine functions
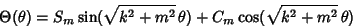 |
(6) |
for 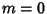 , ...,
, ..., 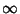 . Plugging (4) into (3) gives
. Plugging (4) into (3) gives
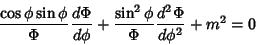 |
(7) |
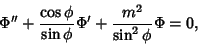 |
(8) |
which is the Legendre Differential Equation for 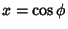 with
with
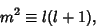 |
(9) |
giving
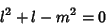 |
(10) |
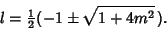 |
(11) |
Solutions are therefore Legendre Polynomials with a Complex index.
The general Complex solution is then
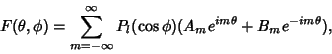 |
(12) |
and the general Real solution is
![\begin{displaymath}
F(\theta,\phi)=\sum_{m=0}^\infty P_l(\cos\phi)[S_m\sin(m\theta)+C_m\cos(m\theta)].
\end{displaymath}](h_1170.gif) |
(13) |
Note that these solutions depend on only a single variable  . However, on the surface of a sphere, it is usual to express
solutions in terms of the Spherical Harmonics derived for the 3-D spherical case, which depend on
the two variables
. However, on the surface of a sphere, it is usual to express
solutions in terms of the Spherical Harmonics derived for the 3-D spherical case, which depend on
the two variables 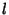 and
and 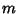 .
.
© 1996-9 Eric W. Weisstein
1999-05-25
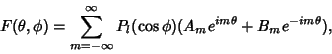
![\begin{displaymath}
F(\theta,\phi)=\sum_{m=0}^\infty P_l(\cos\phi)[S_m\sin(m\theta)+C_m\cos(m\theta)].
\end{displaymath}](h_1170.gif)