|
|
|
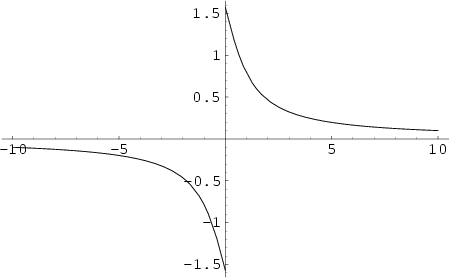

The function ![]() , also denoted arccot(
, also denoted arccot(![]() ), where
), where ![]() is the Cotangent and the superscript
is the Cotangent and the superscript ![]() denotes an
Inverse Function and not the multiplicative inverse. The Maclaurin Series is given by
denotes an
Inverse Function and not the multiplicative inverse. The Maclaurin Series is given by
| (1) |
| (2) |
| (3) |
The inverse cotangent satisfies
| (4) |
| (5) |
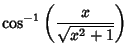 |
(6) | ||
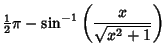 |
(7) | ||
| (8) |
| (9) | |||
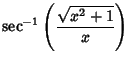 |
(10) | ||
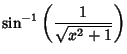 |
(11) | ||
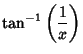 |
(12) |
A number
| (13) |
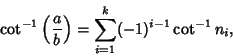 |
(14) |
| (15) |
| (16) | |||
| (17) |
| (18) |
| (19) |
| (20) |
An interesting inverse cotangent identity attributed to Charles Dodgson (Lewis Carroll) by Lehmer (1938b; Bromwich 1965,
Castellanos 1988ab) is
| (21) |
| (22) |
Other inverse cotangent identities include
| (23) |
| (24) |
See also Cotangent, Inverse Tangent, Machin's Formula, Machin-Like Formulas, Tangent
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Inverse Circular Functions.'' §4.4 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 79-83, 1972.
Bennett, A. A. ``The Four Term Diophantine Arccotangent Relation.'' Ann. Math. 27, 21-24, 1926.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 142-143, 1987.
Bromwich, T. J. I. and MacRobert, T. M. An Introduction to the Theory of Infinite Series, 3rd ed. New York: Chelsea, 1991.
Castellanos, D. ``The Ubiquitous Pi. Part I.'' Math. Mag. 61, 67-98, 1988a.
Castellanos, D. ``The Ubiquitous Pi. Part II.'' Math. Mag. 61, 148-163, 1988b.
Lehmer, D. H. ``A Cotangent Analogue of Continued Fractions.'' Duke Math. J. 4, 323-340, 1938a.
Lehmer, D. H. ``On Arccotangent Relations for
Wetherfield, M. ``The Enhancement of Machin's Formula by Todd's Process.'' Math. Gaz., 333-344, July 1996.
![]() .'' Amer. Math. Monthly 45, 657-664, 1938b.
.'' Amer. Math. Monthly 45, 657-664, 1938b.
![]() Weisstein, E. W. ``Arccotangent Series.'' Mathematica notebook CotSeries.m.
Weisstein, E. W. ``Arccotangent Series.'' Mathematica notebook CotSeries.m.
|
|
|
© 1996-9 Eric W. Weisstein