Miquel's Theorem

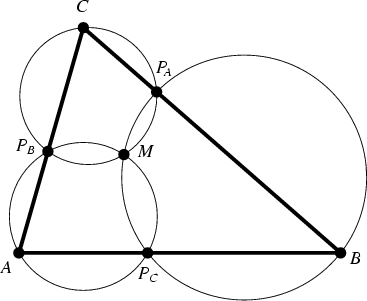
If a point is marked on each side of a Triangle $\Delta ABC$, then the three Miquel Circles (each through a Vertex and the two marked points on the adjacent sides) are Concurrent at a point $M$ called the Miquel Point. This result is a slight generalization of the so-called Pivot Theorem.

If $M$ lies in the interior of the triangle, then it satisfies

$$\angle P_2MP_3=180^\circ-\alpha_1$$

$$\angle P_3MP_1=180^\circ-\alpha_2$$

$$\angle P_1MP_2=180^\circ-\alpha_3.$$

The lines from the Miquel Point to the marked points make equal angles with the respective sides. (This is a by-product of the Miquel Equation.)

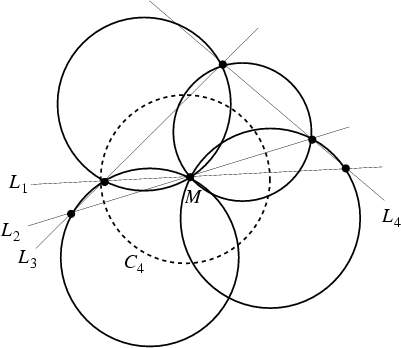
Given four lines $L_1$, ..., $L_4$ each intersecting the other three, the four Miquel Circles passing through each subset of three intersection points of the lines meet in a point known as the 4-Miquel point $M$. Furthermore, the centers of these four Miquel Circles lie on a Circle $C_4$ (Johnson 1929, p. 139). The lines from $M$ to given points on the sides make equal Angles with respect to the sides.

Similarly, given $n$ lines taken by $(n-1)$s yield $n$ Miquel Circles like $C_4$ passing through a point $P_n$, and their centers lie on a Circle $C_{n+1}$.

See also Miquel Circles, Miquel Equation, Miquel Triangle, Nine-Point Circle, Pedal Circle, Pivot Theorem

References

Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, pp. 131-144, 1929.