|
|
|
Partial derivatives are defined as derivatives of a function of multiple variables when all but the variable of interest are held fixed during the differentiation.
| (1) |
For nice functions, mixed partial derivatives must be equal regardless of the order in which the differentiation is performed
so, for example,
| (2) |
| (3) |
| (4) |
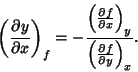 |
(5) |
If the continuity requirement for Mixed Partials is dropped, it is possible to construct functions for which
Mixed Partials are not equal. An example is the function
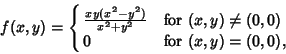 |
(6) |
Abramowitz and Stegun (1972) give Finite Difference versions for partial derivatives.
See also Ablowitz-Ramani-Segur Conjecture, Derivative, Mixed Partial Derivative, Monkey Saddle
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 883-885, 1972.
Fischer, G. (Ed.). Plate 121 in
Mathematische Modelle/Mathematical Models, Bildband/Photograph Volume.
Braunschweig, Germany: Vieweg, p. 118, 1986.
Thomas, G. B. and Finney, R. L. §16.8 in Calculus and Analytic Geometry, 9th ed. Reading, MA: Addison-Wesley, 1996.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 83-85, 1991.
|
|
|
© 1996-9 Eric W. Weisstein