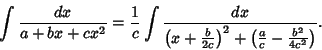To compute an integral of the form
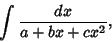 |
(1) |
Complete the Square in the Denominator to obtain
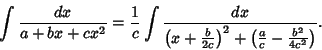 |
(2) |
Let
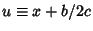 . Then define
. Then define
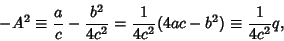 |
(3) |
where
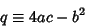 |
(4) |
is the Negative of the Discriminant. If 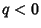 , then
, then
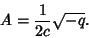 |
(5) |
Now use Partial Fraction Decomposition,
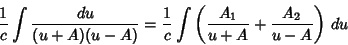 |
(6) |
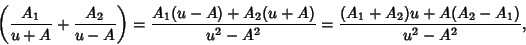 |
(7) |
so
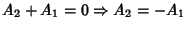 and
and
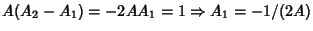 . Plugging these in,
for
. Plugging these in,
for 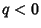 . Note that this integral is also tabulated in Gradshteyn and Ryzhik (1979, equation 2.172), where it is given
with a sign flipped.
. Note that this integral is also tabulated in Gradshteyn and Ryzhik (1979, equation 2.172), where it is given
with a sign flipped.
References
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, 1979.
© 1996-9 Eric W. Weisstein
1999-05-25