|
|
|
The limiting Rabbit Sequence written as a Binary Fraction
![]() (Sloane's A005614), where
(Sloane's A005614), where
![]() denotes a Binary number (a number in base-2). The Decimal value is
denotes a Binary number (a number in base-2). The Decimal value is
Amazingly, the rabbit constant is also given by the Continued Fraction [0, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
...], where
,
...], where ![]() are Fibonacci Numbers with
are Fibonacci Numbers with ![]() taken as 0 (Gardner 1989, Schroeder 1991).
Another amazing connection was discovered by S. Plouffe. Define the Beatty Sequence
taken as 0 (Gardner 1989, Schroeder 1991).
Another amazing connection was discovered by S. Plouffe. Define the Beatty Sequence ![]() by
by
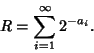
See also Rabbit Sequence, Thue Constant, Thue-Morse Constant
References
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/cntfrc/cntfrc.html
Gardner, M. Penrose Tiles and Trapdoor Ciphers... and the Return of Dr. Matrix, reissue ed.
New York: W. H. Freeman, pp. 21-22, 1989.
Plouffe, S. ``The Rabbit Constant to 330 Digits.''
http://www.lacim.uqam.ca/piDATA/rabbit.txt.
Schroeder, M. Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise. New York: W. H. Freeman, p. 55, 1991.
Sloane, N. J. A.
A005614,
A014565, and
A000201/M2322
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.