An extended Binary Tree satisfying the following conditions:
- 1. Every node has two Children, each colored either red or black.
- 2. Every Leaf node is colored black.
- 3. Every red node has both of its Children colored black.
- 4. Every path from the Root to a Leaf contains the same number (the ``black-height'') of black nodes.
Let 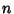 be the number of internal nodes of a red-black tree. Then the number of red-black trees for
be the number of internal nodes of a red-black tree. Then the number of red-black trees for 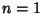 , 2, ... is 2,
2, 3, 8, 14, 20, 35, 64, 122, ... (Sloane's A001131). The number of trees with black roots and red roots are given by
Sloane's A001137 and Sloane's A001138, respectively.
, 2, ... is 2,
2, 3, 8, 14, 20, 35, 64, 122, ... (Sloane's A001131). The number of trees with black roots and red roots are given by
Sloane's A001137 and Sloane's A001138, respectively.
Let 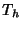 be the Generating Function for the number of red-black trees of black-height
be the Generating Function for the number of red-black trees of black-height 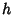 indexed by the number of
Leaves. Then
indexed by the number of
Leaves. Then
![\begin{displaymath}
T_{h+1}(x)=[T_h(x)]^2+[T_h(x)]^4,
\end{displaymath}](r_1025.gif) |
(1) |
where 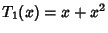 . If
. If 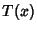 is the Generating Function for the number of red-black trees, then
is the Generating Function for the number of red-black trees, then
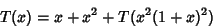 |
(2) |
(Ruskey). Let 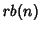 be the number of red-black trees with
be the number of red-black trees with 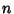 Leaves,
Leaves, 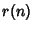 the number of
red-rooted trees, and
the number of
red-rooted trees, and 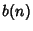 the number of black-rooted trees. All three of the quantities satisfy the Recurrence
Relation
the number of black-rooted trees. All three of the quantities satisfy the Recurrence
Relation
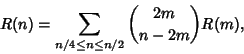 |
(3) |
where 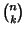 is a Binomial Coefficient,
is a Binomial Coefficient, 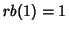 ,
, 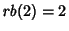 for
for
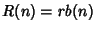 ,
, 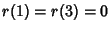 ,
,
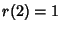 for
for 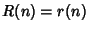 , and
, and 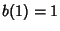 for
for 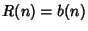 (Ruskey).
(Ruskey).
See also B-Tree
References
Beyer, R. ``Symmetric Binary  -Trees: Data Structures and Maintenance Algorithms.'' Acta Informat. 1, 290-306, 1972.
-Trees: Data Structures and Maintenance Algorithms.'' Acta Informat. 1, 290-306, 1972.
Rivest, R. L.; Leiserson, C. E.; and Cormen, R. H. Introduction to Algorithms. New York: McGraw-Hill, 1990.
Ruskey, F. ``Information on Red-Black Trees.''
http://sue.csc.uvic.ca/~cos/inf/tree/RedBlackTree.html.
Sloane, N. J. A. Sequences
A001131,
A001137, and
A001138
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() be the Generating Function for the number of red-black trees of black-height
be the Generating Function for the number of red-black trees of black-height ![]() indexed by the number of
Leaves. Then
indexed by the number of
Leaves. Then
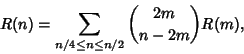
![]() -Trees: Data Structures and Maintenance Algorithms.'' Acta Informat. 1, 290-306, 1972.
-Trees: Data Structures and Maintenance Algorithms.'' Acta Informat. 1, 290-306, 1972.