|
|
|
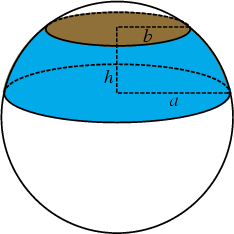
A spherical segment is the solid defined by cutting a Sphere with a pair of Parallel Planes. It can be thought of as a Spherical Cap with the top truncated, and so it corresponds to a Spherical Frustum. The surface of the spherical segment (excluding the bases) is called a Zone.
Call the Radius of the Sphere ![]() and the height of the segment (the distance from the plane to the top of
Sphere)
and the height of the segment (the distance from the plane to the top of
Sphere) ![]() . Let the Radii of the lower and upper bases be denoted
. Let the Radii of the lower and upper bases be denoted ![]() and
and ![]() , respectively.
Call the distance from the center to the start of the segment
, respectively.
Call the distance from the center to the start of the segment ![]() , and the height from the bottom to the top of the segment
, and the height from the bottom to the top of the segment
![]() . Call the Radius parallel to the segment
. Call the Radius parallel to the segment ![]() , and the height above the center
, and the height above the center ![]() . Then
. Then ![]() ,
,
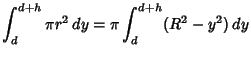 |
|||
| (1) |
| (2) | |||
| (3) |
| (4) | |||
| (5) |
| (6) |
| (7) |
See also Archimedes' Problem, Frustum, Hemisphere, Sphere, Spherical Cap, Spherical Sector, Surface of Revolution, Zone
References
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 130, 1987.
|
|
|
© 1996-9 Eric W. Weisstein