|
|
|
The sequence defined by ![]() and the Recurrence Relation
and the Recurrence Relation
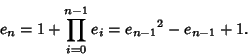 |
(1) |
| (2) |
| (3) |
| (4) |
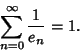 |
(5) |
The ![]() of the first few Prime
of the first few Prime ![]() are 0, 1, 2, 3, 5, .... Vardi (1991) gives a lists of factors less than
are 0, 1, 2, 3, 5, .... Vardi (1991) gives a lists of factors less than ![]() of
of ![]() for
for ![]() and shows that
and shows that ![]() is Composite for
is Composite for
![]() . Furthermore,
all numbers less than
. Furthermore,
all numbers less than
![]() in Sylvester's sequence are Squarefree, and no Squareful
numbers in this sequence are known (Vardi 1991).
in Sylvester's sequence are Squarefree, and no Squareful
numbers in this sequence are known (Vardi 1991).
See also Euclid's Theorems, Greedy Algorithm, Squarefree, Squareful
References
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Research problem 4.65 in
Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994.
Sloane, N. J. A. Sequence
A000058/M0865
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Vardi, I. ``Are All Euclid Numbers Squarefree?'' and ``PowerMod to the Rescue.'' §5.1 and 5.2 in
Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 82-89, 1991.
|
|
|
© 1996-9 Eric W. Weisstein