|
|
|
A second-Rank symmetric Tensor is defined as a Tensor ![]() for which
for which
| (1) |
| (2) |
| (3) |
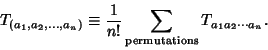 |
(4) |
The product of a symmetric and an Antisymmetric Tensor is 0. This can be seen as follows. Let
![]() be Antisymmetric, so
be Antisymmetric, so
| (5) |
| (6) |
| (7) |
| (8) |
A symmetric second-Rank Tensor ![]() has Scalar invariants
has Scalar invariants
| (9) | |||
| (10) |
|
|
|
© 1996-9 Eric W. Weisstein