|
|
|
Although Bessel Functions of the Second Kind are sometimes called
Weber functions, Abramowitz and Stegun (1972) define a separate Weber function as
| (1) |
Letting
![]() be a Root of Unity, another set of Weber functions is defined as
be a Root of Unity, another set of Weber functions is defined as
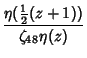 |
(2) | ||
| (3) | |||
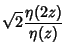 |
(4) | ||
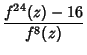 |
(5) | ||
![$\displaystyle {[f^{24}(z)+8][{f_1}^8(z)-{f_2}^8(z)]\over f^8(z)}$](w_401.gif) |
(6) |
| (7) | |||
| (8) | |||
| (9) | |||
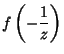 |
(10) | ||
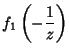 |
(11) | ||
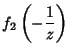 |
(12) |
See also Anger Function, Bessel Function of the Second Kind, Dedekind Eta Function, j-Function, Jacobi Identities, Jacobi Triple Product, Modified Struve Function, Q-Function, Struve Function
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Anger and Weber Functions.'' §12.3 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 498-499, 1972.
Atkin, A. O. L. and Morain, F. ``Elliptic Curves and Primality Proving.'' Math. Comput. 61, 29-68, 1993.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity.
New York: Wiley, pp. 68-69, 1987.
Weber, H. Lehrbuch der Algebra, Vols. I-II. New York: Chelsea, pp. 113-114, 1902.
|
|
|
© 1996-9 Eric W. Weisstein