Witch of Agnesi

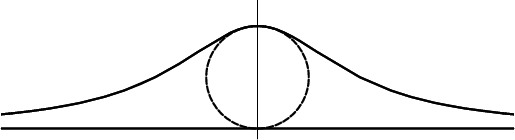
A curve studied and named ``versiera'' (Italian for ``she-devil'' or ``witch'') by Maria Agnesi in 1748 in her book Istituzioni Analitiche (MacTutor Archive). It is also known as Cubique d'Agnesi or Agnésienne. Some suggest that Agnesi confused an old Italian word meaning ``free to move'' with another meaning ``witch.'' The curve had been studied earlier by Fermat and Guido Grandi in 1703.

It is the curve obtained by drawing a line from the origin through the Circle of radius $a$ ($OB$), then picking the point with the $y$ coordinate of the intersection with the circle and the $x$ coordinate of the intersection of the extension of line $OB$ with the line $y=2a$. The curve has Inflection Points at $y = 3a/2$. The line $y = 0$ is an Asymptote to the curve.

In parametric form,

$$x = 2a\cot\theta$$ (1)

$$y = a[1-\cos(2\theta)],$$ (2)

or

$$x = 2at$$ (3)

$$y = {2a\over 1+t^2}.$$ (4)

In rectangular coordinates,

$$y={8a^3\over x^2+4a^2}.$$ (5)

See also Lamé Curve

References

Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 90-93, 1972.

Lee, X. ``Witch of Agnesi.'' http://www.best.com/~xah/SpecialPlaneCurves_dir/WitchOfAgnesi_dir/witchOfAgnesi.html

MacTutor History of Mathematics Archive. ``Witch of Agnesi.'' http://www-groups.dcs.st-and.ac.uk/~history/Curves/Witch.html.

Yates, R. C. ``Witch of Agnesi.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 237-238, 1952.