|
|
|
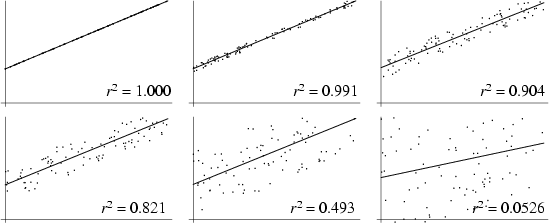
The correlation coefficient is a quantity which gives the quality of a Least Squares Fitting to the original
data. To define the correlation coefficient, first consider the sum of squared values ![]() ,
, ![]() , and
, and
![]() of a set of
of a set of ![]() data points
data points ![]() about their respective means,
about their respective means,
| (1) | |||
| (2) | |||
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
The correlation coefficient ![]() (sometimes also denoted
(sometimes also denoted ![]() ) is then defined by
) is then defined by
![\begin{displaymath}
r\equiv \sqrt{bb'} = {n\sum xy-\sum x\sum y\over \sqrt{\left...
...)^2}\right]\left[{n\sum y^2-\left({\sum y}\right)^2}\right]}},
\end{displaymath}](c3_201.gif) |
(8) |
| (9) |
The correlation coefficient has an important physical interpretation. To see this, define
| (10) |
| (11) | |||
| (12) | |||
| (13) | |||
| (14) |
 |
|||
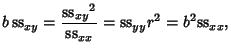 |
(15) |
| (16) |
| (17) | |||
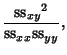 |
(18) |
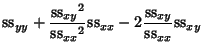 |
|||
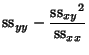 |
(19) | ||
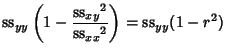 |
|||
| (20) |
| (21) |
The square of the correlation coefficient ![]() is therefore given by
is therefore given by
| (22) |
If there is complete correlation, then the lines obtained by solving for best-fit ![]() and
and ![]() coincide
(since all data points lie on them), so solving (6) for
coincide
(since all data points lie on them), so solving (6) for ![]() and equating to (4) gives
and equating to (4) gives
| (23) |
| (24) |
The correlation coefficient is independent of both origin and scale, so
| (25) |
| (26) | |||
| (27) |
See also Correlation Index, Correlation Coefficient--Gaussian Bivariate Distribution, Correlation Ratio, Least Squares Fitting, Regression Coefficient
References
Acton, F. S. Analysis of Straight-Line Data. New York: Dover, 1966.
Kenney, J. F. and Keeping, E. S. ``Linear Regression and Correlation.'' Ch. 15 in Mathematics of Statistics, Pt. 1, 3rd ed.
Princeton, NJ: Van Nostrand, pp. 252-285, 1962.
Gonick, L. and Smith, W. The Cartoon Guide to Statistics. New York: Harper Perennial, 1993.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Linear Correlation.'' §14.5 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 630-633, 1992.
|
|
|
© 1996-9 Eric W. Weisstein