|
|
|
Elliptic alpha functions relate the complete Elliptic Integrals of the First ![]() and
Second Kinds
and
Second Kinds ![]() at Elliptic Integral Singular Values
at Elliptic Integral Singular Values ![]() according to
according to
![$\displaystyle {E'(k_r)\over K(k_r)}-{\pi\over 4[K(k_r)]^2}$](e_714.gif) |
(1) | ||
![$\displaystyle {\pi\over 4[K(k_r)]^2}+\sqrt{r}-{E(k_r)\sqrt{r}\over K(k_r)}$](e_715.gif) |
(2) | ||
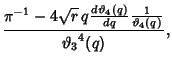 |
(3) |
| (4) | |||
| (5) |
| (6) |
| (7) |
| (8) |
![\begin{eqnarray*}
\alpha(1)&=&{\textstyle{1\over 2}}\\
\alpha(2)&=&\sqrt{2}-1...
...]\\
\alpha(27)&=&3[{\textstyle{1\over 2}}(\sqrt{3}+1)-2^{1/3}]
\end{eqnarray*}](e_726.gif)
![\begin{eqnarray*}
\alpha(30)&=&{\textstyle{1\over 2}}\{\sqrt{30} - (2 + \sqrt{5...
...(\sqrt{8}-1)-(2^{1/4}-1)^4]\over (\sqrt{\sqrt{2}+1}+2^{5/8})^4}.
\end{eqnarray*}](e_727.gif)
J. Borwein has written an Algorithm which uses lattice basis reduction to provide algebraic values for ![]() .
.
See also Elliptic Integral of the First Kind, Elliptic Integral of the Second Kind, Elliptic Integral Singular Value, Elliptic Lambda Function
References
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity.
New York: Wiley, 1987.
Borwein, J. M.; Borwein, P. B.; and Bailey, D. H. ``Ramanujan, Modular Equations, and Approximations
to Pi, or How to Compute One Billion Digits of Pi.'' Amer. Math. Monthly 96, 201-219, 1989.
![]() Weisstein, E. W. ``Elliptic Singular Values.'' Mathematica notebook EllipticSingular.m.
Weisstein, E. W. ``Elliptic Singular Values.'' Mathematica notebook EllipticSingular.m.
|
|
|
© 1996-9 Eric W. Weisstein