|
|
|
The special unitary group ![]() is the set of
is the set of ![]() Unitary Matrices with
Determinant
Unitary Matrices with
Determinant ![]() (having
(having ![]() independent parameters).
independent parameters). ![]() is Homeomorphic with the
Orthogonal Group
is Homeomorphic with the
Orthogonal Group ![]() . It is also called the Unitary Unimodular Group and is a Lie Group. The
special unitary group can be represented by the Matrix
. It is also called the Unitary Unimodular Group and is a Lie Group. The
special unitary group can be represented by the Matrix
| (1) |
| (2) |
![$\displaystyle \left[\begin{array}{cc}\cos({\textstyle{1\over 2}}\phi) & i\sin({...
...\textstyle{1\over 2}}\phi) & \cos({\textstyle{1\over 2}}\phi)\end{array}\right]$](s2_610.gif) |
(3) | ||
![$\displaystyle \left[\begin{array}{cc}\cos({\textstyle{1\over 2}}\beta) & \sin({...
...extstyle{1\over 2}}\beta) & \cos({\textstyle{1\over 2}}\beta)\end{array}\right]$](s2_612.gif) |
(4) | ||
![$\displaystyle \left[\begin{array}{cc}e^{i\xi} & 0 \\ 0 & e^{-i\xi} \end{array}\right].$](s2_614.gif) |
(5) |
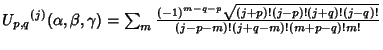
|
|
|
|
(6) |
![$\displaystyle \left\{\begin{array}{ll} 1+2\cos\alpha + \ldots + 2\cos(j\alpha) ...
...{\textstyle{3\over 2}}\alpha)+\ldots+\cos(j\alpha)] & \mbox{}\end{array}\right.$](s2_620.gif) |
|||
![$\displaystyle \left\{\begin{array}{ll} {\sin[(j+{\textstyle{1\over 2}})\alpha]\...
...= {\textstyle{1\over 2}}, {\textstyle{3\over 2}}, \ldots.$\ }\end{array}\right.$](s2_621.gif) |
(7) |
See also Orthogonal Group, Special Linear Group, Special Orthogonal Group
References
Arfken, G. ``Special Unitary Group,
Conway, J. H.; Curtis, R. T.; Norton, S. P.; Parker, R. A.; and Wilson, R. A.
``The Groups
![]() and
and ![]() -
-![]() Homomorphism.''
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 253-259, 1985.
Homomorphism.''
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 253-259, 1985.
![]() ,
, ![]() ,
,
![]() , and
, and
![]() .'' §2.2 in
Atlas of Finite Groups: Maximal Subgroups and Ordinary Characters for Simple Groups. Oxford, England:
Clarendon Press, p. x, 1985.
.'' §2.2 in
Atlas of Finite Groups: Maximal Subgroups and Ordinary Characters for Simple Groups. Oxford, England:
Clarendon Press, p. x, 1985.
|
|
|
© 1996-9 Eric W. Weisstein