|
|
|
The 3-D analog of the Sierpinski Sieve illustrated above, also called the
Sierpinski Sponge or Sierpinski Tetrahedron. Let ![]() be the number of tetrahedra,
be the number of tetrahedra, ![]() the length of a side, and
the length of a side, and ![]() the fractional Volume of tetrahedra after the
the fractional Volume of tetrahedra after the
![]() th iteration. Then
th iteration. Then
| (1) | |||
| (2) | |||
| (3) |
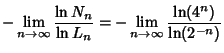 |
|||
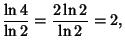 |
(4) |
The following illustration demonstrates how this counterintuitive fact can be true by showing three stages of the rotation of a tetrix, viewed along one of its edges. In the last frame, the tetrix ``looks'' like the 2-D Plane.
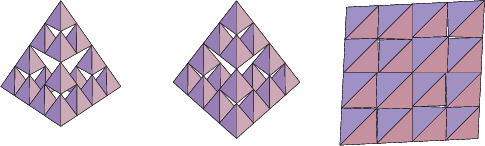
See also Menger Sponge, Sierpinski Sieve
References
Dickau, R. M. ``Sierpinski Tetrahedron.''
http://forum.swarthmore.edu/advanced/robertd/tetrahedron.html.
Eppstein, D. ``Sierpinski Tetrahedra and Other Fractal Sponges.''
http://www.ics.uci.edu/~eppstein/junkyard/sierpinski.html.
|
|
|
© 1996-9 Eric W. Weisstein